Standard #: MA.8.F.1.2


This document was generated on CPALMS - www.cpalms.org



Given a function defined by a graph or an equation, determine whether the function is a linear function. Given an input-output table, determine whether it could represent a linear function.


Clarifications


Clarification 1: Instruction includes recognizing that a table may not determine a function.

General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 8
Strand: Functions
Standard: Define, evaluate and compare functions.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Function
  • Linear Function

 

Vertical Alignment

Previous Benchmarks

Next Benchmarks

 

Purpose and Instructional Strategies

In grade 7, students determined whether a relationship was proportional, given a table, equation or written description. In grade 8, students determine whether the function defined by a graph or an equation is a linear function. In Algebra 1, students will classify the function type given an equation or graph and compare key features of linear and nonlinear functions.
  • Instruction includes determining if the function has a constant rate of change between the x- and y-values.
    • For example, students can depict the rate of change between the values in a table like below.
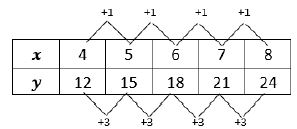
      Table
  • Instruction includes a focus on the connection between the equation and the graph.
  • Students should develop an understanding of a linear function by using examples and non-examples.
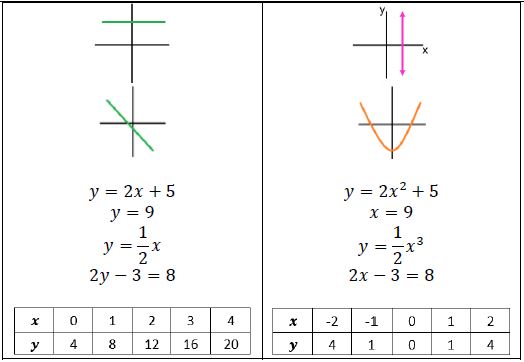
    Table
    Table

 

Common Misconceptions or Errors

  • Students may not understand the connection from a table to the visual of a graph of the same function. To address this misconception, provide opportunities for students to make connections and see the graph and table side by side.

 

Strategies to Support Tiered Instruction

  • Teacher models how to get from a set of points displayed on a table to the points graphed on a coordinate plane, and how points from a coordinate plan can be written in a table. Then, teacher provides opportunities to notice any patterns in the graph or table that will help identify if the function is linear.
  • Teacher co-constructs a graph from a table with students, as well as a table from a graph to increase understanding of the relationship between the two. Once students become comfortable moving between graphs and tables, students can begin inspecting tables that represent functions. Teachers can review proportional and linear relationships and work with students to dissect tables to find if they contain a proportional relationship, meaning they are linear. Students should note that not all linear relationships are proportional, but all proportional relationships are linear.
  • Teacher provides opportunities for students to make connections and see the graph and table of the same function side by side.

 

Instructional Tasks

Instructional Task 1 (MTR.6.1)
The area, A, of an isosceles right triangle is a function of the length of its legs, s, and is represented by the equation A = 0.5s².
  • Part A. Create a table of values to represent this function.
  • Part B. Plot the points on a coordinate plane.
  • Part C. What is the domain and range of the function?
  • Part D. Is this function linear or nonlinear? Explain and justify your answer.

Instructional Task 2 (MTR.2.1)
Part A. Create a table that could represent a linear function.
Part B. Create a table that could represent a non-linear function.
Part C. Compare your table from Part B with a partner.

 

Instructional Items

Instructional Item 1
Taro and Jiro climbed a mountain and hiked back down. At the summit and at every station along the way back down, they recorded their altitude and the amount of time they had been travelling. Can the data in the table represent a linear function?
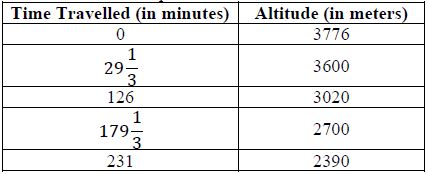
Table with altitude in meters and amount of time travelled in minutes

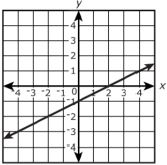
Instructional Item 2
Does the graph below represent a linear function? If so, justify your answer.
Graph

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.



Related Courses

Course Number1111 Course Title222
1205050: M/J Accelerated Mathematics Grade 7 (Specifically in versions: 2014 - 2015, 2015 - 2020, 2020 - 2022, 2022 - 2024, 2024 and beyond (current))
1205070: M/J Grade 8 Pre-Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
1204000: M/J Foundational Skills in Mathematics 6-8 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7812030: Access M/J Grade 8 Pre-Algebra (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.8.F.1.AP.2 Given a function displayed on a graph or an equation, identify whether the function is a linear function.


Related Resources

Formative Assessments

Name Description
What Am I?

Students are asked to describe a linear function, its graph, and the meaning of its parameters.

Linear or Nonlinear?

Students are asked to identify a function as either linear or nonlinear and to justify their decision.

Explaining Linear Functions

Students are asked to describe defining properties of linear functions.

Lesson Plans

Name Description
What's My Function?

Students will determine function rules that have been written on cards taped to their backs. They will suggest input values and peers will provide output values to help them determine their function. They will then graph their functions for additional practice.

An Introduction to Functions: How Much Are Playoff Tickets?

This lesson introduces functions with the real-world example of the cost of tickets for a playoff game. Also, students will determine if tables, graphs, or sets of ordered pairs represent linear functions and explain their reasoning.

Functions With Vertical Line Test!

This is an introductory lesson on functions. Students will review how to graph ordered pairs and learn how to use a function table. In addition, students learn the difference between functions and nonfunctions and how to distinguish between the two.

Getting Graphic with Linear Functions

Students will determine whether a function defined by a graph or an equation is a linear function, determine the rates of change and initial value from a table and graph, as well as be able to interpret what the rate of change means as it relates to a situation.

The Linear Function Connection

The students will compare two linear functions that have been represented in different ways (equation, table, graph, verbal description). They will be able to find and compare the rate of change, or slope, of the function from any of the representations.

In the Real World

This resource provides a Lesson Plan for teaching students how to analyze real-world problems to look for clearly identified values and determine which of them is a constant value and which of them is subject to change (will increase or decrease per unit of time, weight, length, etc.). The students will also be taught how to determine the correct units for each value in an equation written in slope-intercept form.

Functions: Are They Linear or Non-Linear?

In this lesson, students will investigate 5 different functions to see if they are linear or non-linear. They will then analyze the functions in groups. After that they will present their results and reasoning.

Function or No Function?

This resource provides a lesson plan for teaching students how to recognize relations and functions. They will distinguish which relations are functions and which are not.

How Much is My Cell Phone Plan?

In this lesson, shopping for cell phone plans provides a motivating context where students will compare and interpret the properties of two functions represented in different ways. The lesson starts with students examining and discussing an input/output table to identify rate of change and y-intercept. Students will each be assigned a group. Groups will solve two different problems involving cell phone plans. They must determine the rate of change, y-intercept, and the total cost after two years. Students will receive homework and have a summative assessment the next day.

What Are My Test Scores?

Students will define what a function is at the beginning of class. They will activate prior knowledge by playing "Four Corners." After that, there will be an investigation of what a function is and how it relates to the total questions on an assessment and the point value for each question. Then, students will analyze different assessments. and present their findings. For homework, students will have practice problems.

Original Student Tutorials

Name Description
Cruising Through Functions

Cruise along as you discover how to qualitatively describe functions in this interactive tutorial.

Summer of FUNctions

Have some fun with FUNctions! Learn how to identify linear and non-linear functions in this interactive tutorial.

Virtual Manipulative

Name Description
Functions and Vertical Line Test

This lesson is designed to introduce students to the vertical line test for functions as well as practice plotting points and drawing simple functions. The lesson provides links to discussions and activities related to the vertical line test and functions as well as suggested ways to integrate them into the lesson.

Student Resources

Original Student Tutorials

Name Description
Cruising Through Functions:

Cruise along as you discover how to qualitatively describe functions in this interactive tutorial.

Summer of FUNctions:

Have some fun with FUNctions! Learn how to identify linear and non-linear functions in this interactive tutorial.



Printed On:4/4/2025 3:13:44 AM
Print Page | Close this window