General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- NA
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
Students are building on their ability to write and verify solutions in inequalities in grade 6 to now write and solve one-step inequalities in one variable (MTR.5.1). In grade 8, students will solve two-step linear inequalities in one variable.- Instruction includes real-world scenarios to assist students with making sense of solving inequalities by checking the reasonableness of their answer.
- Instruction emphasizes properties of inequality with connections to the properties of equality (MTR.5.1).
- Instruction includes showing why the inequality symbol reverses when multiplying or dividing both sides of an inequality by a negative number.
- For example, if the inequality 6 > −7 is multiplied by −3, it results in −18 > 21 which is a false statement. The inequality symbol must be reversed in order to keep a true statement. Since 6 is to the right of -7 on the number line and multiplying by a negative number reverses directions, 6(−3) will be to the left of −7(−3) on the number line.
- Instruction includes cases where the variable is on the left side or the right side of the inequality.
- Variables are not limited to . Instruction includes using a variety of lowercase letters for their variables; however , and should be avoided as they too closely resemble zero and one.
- Instruction emphasizes the understanding of defining an algebraic inequality. Students should have practice with inequalities in the form of > , < , ≥ and ≤ . Students should explore how “is greater than or equal to” and “is strictly greater than” are similar and different as well as “is less than or equal to” and “is strictly less than.” Students should use academic language when describing the algebraic inequality.
Common Misconceptions or Errors
- Students may confuse when to use an open versus closed circle when graphing an inequality. Emphasize the inclusion (≤ and ≥) versus non-inclusion (< and >) of that value as a viable solution and provide problems that motivate reasoning with different ranges of possible values for the variable.
- Some students are unable to see the difference between the division property of equality and the division property of inequality.
- Students may mistakenly think that the direction the inequality symbol is pointing is always the direction they shade on the number line. To address this misconception, emphasize reading the inequality sentence aloud and use numerical examples to test for viable solutions (MTR.6.1).
Strategies to Support Tiered Instruction
- Teacher provides instruction on when to use an open versus closed circle when graphing an inequality. Teacher encourages students to substitute their solution into their graphs and discuss whether their graph makes sense with the solution.
- Teacher provides a graphic organizer with examples and non-examples of the Division Property of Equality and the Division Property of Inequality.
- Teacher provides students with pre-drawn number lines for students to number as needed to graph solutions.
- Teacher provides students with instruction for similarities and differences of solving equations versus solving inequalities.
- Teacher emphasizes reading the inequality sentence aloud and use numerical examples to test for solutions.
- Instruction includes emphasizing the inclusion (≤ and ≥) versus non-inclusion (< and >) of that value as a solution and provide problems that motivate reasoning with different ranges of possible values for the variable.
- For example, if the given inequality is + 3 > 5, students can test various numbers to determine if they are solutions. When students test = 2, students should realize that they get the inequality 5 > 5 which is not a true statement, therefore 2 is not a solution.
Instructional Tasks
Instructional Task 1 (MTR.3.1, MTR.4.1)Determine if there is an error in each of the following. If there is an error, write the corrected
solution. If there is not an error, indicate “No Error” next to the answer.

Using integers between −5 and 5 no more than once, finish writing the inequality below, whose solutions are ≥ .
Instructional Items
Instructional Item 1Solve the inequality and graph its solutions on a number line.
Instructional Item 2
What are the solutions to the inequality 4.2 +
Instructional Item 3
Represent the solutions to the inequality −0.125
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.

 ;
;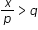 ; x±p>q and p±x>q, where p and q are specific rational numbers and any inequality symbol can be represented.
; x±p>q and p±x>q, where p and q are specific rational numbers and any inequality symbol can be represented.