Rewrite rational numbers in different but equivalent forms including fractions, mixed numbers, repeating decimals and percentages to solve mathematical and real-world problems.
and his calculator gives him the answer 5.6666666667. Justin makes the statement that
; is he correct?
| Name |
Description |
| The Watergate Effect part 3 | Students will create a circle graph to display categorical data of the public presidential approval rates after the Supreme Court Case United States v. Nixon. Students will graph results independently and compare them to the circle graphs created during the Watergate Effect Part 1 Lesson (Resource ID#: 208926) and the Watergate Effect Part 2 Lesson (Resource ID#: 210122) to discuss the trend of the data over the entirety of the Supreme Court case. |
| The Watergate Effect part 2 | Students will create a circle graph to display categorical data of the public presidential approval rates during the Supreme Court Case United States v. Nixon. Students will graph results in pairs/groups and compare them to the circle graph created during the Watergate Effect Part 1 Lesson (Resource ID#: 208926). |
| Generating Equivalent Forms of Numbers Using the Legislative Branch of the Government | Students will rewrite fractions, decimals, and percentages in equivalent forms to compare the number of seats that each state has in the U.S. House of Representatives to the total number of seats in the House of Representatives, in this integrated lesson plan. |
| The Watergate Effect Part 1 | Students will create a circle graph to display categorical data of the public presidential approval rates of Richard Nixon before the Supreme Court Case United States v. Nixon. Students will calculate percentages and central angle degrees to graph results in pairs/groups and analyze the results in this integrated lesson plan. |
| Fractions and Percentages of the Legislative Branch | Students will use fractions, decimals, and percentages to compare the number of seats that Florida (as well as other states) has in the U.S. House of Representatives to the total amount of seats in the House of Representatives in this integrated lesson plan. |
| Rewriting Rational Numbers to Analyze International Organizations (Part 1: United Nations) | Students will analyze regional membership of the United Nations to represent the part to a whole relationship as a fraction. Students will rewrite rational numbers in equivalent forms while examining the purpose of the United Nations and the United States’ role as a member in this integrated lesson plan. |
| Independent Compound Probability | During this lesson, students will use Punnett Squares to determine the probability of an offspring's characteristics. |
| Fast Food Frenzy | In this activity, students will engage critically with nutritional information and macronutrient content of several fast food meals. This is an MEA that requires students to build on prior knowledge of nutrition and working with percentages. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| "Ad" it Up | Students will learn how to calculate markup, markdown, percent increase, and percent decrease. Using sales "ad" inserts from the internet, newspapers, and store flyers, students will understand how these concepts apply to real-world situations. |
| Who's Being Irrational? | In this lesson, students will learn how irrational numbers differ from rational numbers. The students will complete a graphic organizer that categorizes rational and irrational numbers. Students will also be able to identify irrational numbers found in the real world. |
| Savvy Shopping | This is the second part of the CPalms lesson titled Markup and Make Money. In Savvy Shopping students will shop at their peers' store and buy items. If it is discounted, they will have to calculate the revised price. They will then find the total price including the tax. |
| Shopping the Ads | Have you ever heard students ask the question, "Why do I have to learn this?" This lesson answers that question because it requires the students to apply their knowledge in real world scenarios but does not teach a basic conceptual understanding of percentages. The teacher may use the whole lesson or select specific problems. |
| Rational vs Irrational | Students will organize the set of real numbers and be able to identify when a number is rational or irrational. They will also learn the process of how to change a repeating decimal to its equivalent fraction. |
| Beads in a Bowl | This activity will allow students to explore the concept of simple probability using a random selection of multi-colored beads. |
| Markup and Make Money | In this lesson students will create their own imaginary store with at least 15 items to sell. They will begin with a discussion and then learn about markup. They will use their knowledge to calculate prices and create a display for their store. This is the first of 2 lessons (next lesson is Savvy Shopping, Resource ID 48879), which allows students to shop in their peer's store to calculate discount and tax. |
| Really! I'm Rational! | In this lesson students will gain an understanding of how repeating decimals are converted into a ratio in the form of  by completing an exploration worksheet. They will conclude that any number which can be written in this form is called a rational number. by completing an exploration worksheet. They will conclude that any number which can be written in this form is called a rational number. |
| Name |
Description |
| Equivalent fractions approach to non-repeating decimals | The purpose of the task is to get students to reflect on the definition of decimals as fractions (or sums of fractions), at a time when they are seeing them primarily as an extension of the base-ten number system and may have lost contact with the basic fraction meaning. Students also have their understanding of equivalent fractions and factors reinforced. |
| Repeating Decimal as Approximation | The student is asked to complete a long division which results in a repeating decimal, and then use multiplication to "check" their answer. The purpose of the task is to have students reflect on the meaning of repeating decimal representation through approximation. |
| Estimating Square Roots | By definition, the square root of a number n is the number you square to get n. The purpose of this task is to have students use the meaning of a square root to find a decimal approximation of a square root of a non-square integer. Students may need guidance in thinking about how to approach the task. |
| Converting Decimal Representations of Rational Numbers to Fraction Representations | Requires students to "convert a decimal expansion which repeats eventually into a rational number." Despite this choice of wording, the numbers in this task are rational numbers regardless of the choice of representation. For example, 0.333¯ and 1/3 are two different ways of representing the same number. |
| Calculating and Rounding Numbers | In this task, students explore some important mathematical implications of using a calculator. Specifically, they experiment with the approximation of common irrational numbers such as pi (p) and the square root of 2 (v2) and discover how to properly use the calculator for best accuracy. Other related activities involve converting fractions to decimal form and a concrete example where rounding and then multiplying does not yield the same answer as multiplying and then rounding. |
| Name |
Description |
| Repeating Decimal as Approximation: | The student is asked to complete a long division which results in a repeating decimal, and then use multiplication to "check" their answer. The purpose of the task is to have students reflect on the meaning of repeating decimal representation through approximation. |
| Estimating Square Roots: | By definition, the square root of a number n is the number you square to get n. The purpose of this task is to have students use the meaning of a square root to find a decimal approximation of a square root of a non-square integer. Students may need guidance in thinking about how to approach the task. |
| Converting Decimal Representations of Rational Numbers to Fraction Representations: | Requires students to "convert a decimal expansion which repeats eventually into a rational number." Despite this choice of wording, the numbers in this task are rational numbers regardless of the choice of representation. For example, 0.333¯ and 1/3 are two different ways of representing the same number. |
| Name |
Description |
| Repeating Decimal as Approximation: | The student is asked to complete a long division which results in a repeating decimal, and then use multiplication to "check" their answer. The purpose of the task is to have students reflect on the meaning of repeating decimal representation through approximation. |
| Estimating Square Roots: | By definition, the square root of a number n is the number you square to get n. The purpose of this task is to have students use the meaning of a square root to find a decimal approximation of a square root of a non-square integer. Students may need guidance in thinking about how to approach the task. |
| Converting Decimal Representations of Rational Numbers to Fraction Representations: | Requires students to "convert a decimal expansion which repeats eventually into a rational number." Despite this choice of wording, the numbers in this task are rational numbers regardless of the choice of representation. For example, 0.333¯ and 1/3 are two different ways of representing the same number. |
| Calculating and Rounding Numbers: | In this task, students explore some important mathematical implications of using a calculator. Specifically, they experiment with the approximation of common irrational numbers such as pi (p) and the square root of 2 (v2) and discover how to properly use the calculator for best accuracy. Other related activities involve converting fractions to decimal form and a concrete example where rounding and then multiplying does not yield the same answer as multiplying and then rounding. |

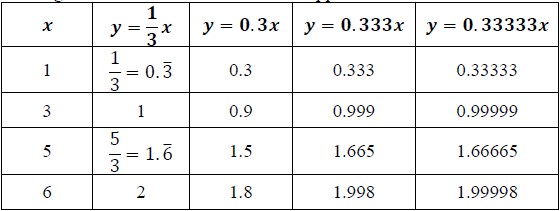
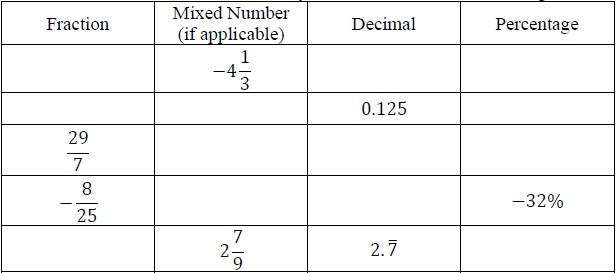

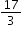 and his calculator gives him the answer 5.6666666667. Justin makes the statement that
and his calculator gives him the answer 5.6666666667. Justin makes the statement that 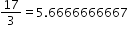 ; is he correct?
; is he correct?  by completing an exploration worksheet. They will conclude that any number which can be written in this form is called a rational number.
by completing an exploration worksheet. They will conclude that any number which can be written in this form is called a rational number.