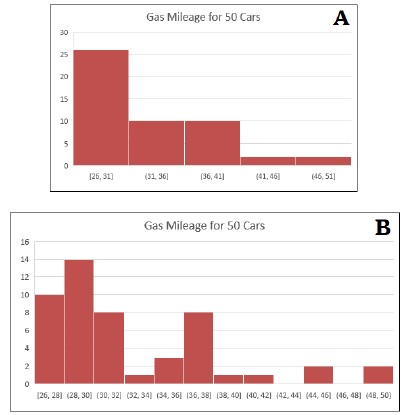
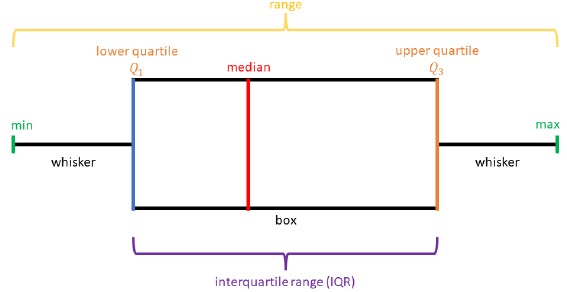
Create box plots and histograms to represent sets of numerical data within real-world contexts.
The numerical data set {15,0,32,24,0,17,42,0,29,120,0,20}, collected based on minutes spent on homework, can be represented graphically using a box plot.
Instruction includes collecting data and discussing ways to collect truthful data to construct graphical representations.
| Name |
Description |
| Using Box Plots and the Mean Absolute Deviation to Interpret Data | This lesson explores the use of box plots and the mean absolute deviation to compare two data sets and draw inferences. |
| Measurement Data Error | In this interdisciplinary lesson, students will practice the skill of data collection with a variety of tools and by statistically analyzing the class data sets will begin to understand that error is inherent in all data. |
| Analyzing Box Plots | This lesson is designed for students to demonstrate their knowledge of box plots.
- Students will need to create four box plots from given data.
- Students will need to analyze the data displayed on the box plots by comparing similarities and differences.
- Students will work with a partner to complete the displays and the follow-up questions.
|
| Exercise Your Brain, Analyze Your Heart Rate | Students will compile the data gathered from measuring their resting heart rates and heart rates after exercising into box plots. Using these displays, they will analyze the data's center, shape, and spread. |
| Bowling for Box Plots | Students will learn about the effects of an outlier and interpret differences in shape, center, and spread using a bowling activity to gather data. The students will learn to score their games, report their scores, and collectively measure trends and spread by collaborating to create a box plot. They will analyze and compare box plots, and determine how much of an effect an extreme score (outlier) can have on the overall box plot of the data. |
| What's My Grade? | "What's My Grade" is a lesson that will focus on a sample student's grades to demonstrate how a final grade is calculated as well as explore possible future grades. Students will create the distributions of each grade category using histograms. They will also analyze grades using mean and standard deviation. Students will use statistics to determine data distribution while comparing the center and spread of two or more different data sets. |
| How tall is an 8th grader? | Ever wonder about the differences in heights between students in grade 8? In this lesson, students will use data they collect to create and analyze multiple box plots using 5-number summaries. Students will make inferences about how height and another category may or may not be related. |
| Plane Statistics | This lesson starts with an activity to gather data using paper airplanes then progresses to using appropriate statistics to compare the center and spread of the data. Box plots are used in this application lesson of concepts and skills previously acquired. |
| Which One: Box plot, Dot Plot, or Histogram? | Students will be asked to obtain data and create a human box plot, which will be analyzed and explained using statistical terms. Students will then understand the differences and advantages to using the box plot, histogram, and dot plot. Students will also practice selecting the most appropriate graphical representation for a set of data. |
| What's Your Tendency? | This resource can be used to teach students how to create and compare box plots. After completing this lesson, students should be able to answer questions in both familiar and unfamiliar situations. |
| The Distance a Coin Will Travel | This lesson is a hands-on activity that will allow students to collect and display data about how far different coins will travel. The data collected is then used to construct double dot plots and double box plots. This activity helps to facilitate the statistical implications of data collection and the application of central tendency and variability in data collection. |
| Which is Better? Using Data to Make Choices | Students use technology to analyze measures of center and variability in data. Data displays such as box plots, line plots, and histograms are used. The effects of outliers are taken into consideration when drawing conclusions. Students will cite evidence from the data to support their conclusions. |
| How long did you study? | Students will create and analyze histograms based on student study time when preparing for the Algebra EOC. Students will be given a set of data and guided notes |
| How many licks does it take to get to the center? | Students will create different displays, line plots, histograms, and box plots from data collected about types of lollipops. The data will be analyzed and compared. Students will determine "Which lollipop takes the fewest number of licks to get to the center: a Tootsie Pop, a Blow Pop, or a Dum Dum?" |
| Birthday Party Decisions | Students will create and compare four different boxplots to determine the best location for a birthday party. |
| Outliers in the Outfield – Dealing With Extreme Data Points | Students will explore the effects outliers have on the mean and median values using the Major League Baseball (MLB) salary statistics. They will create and compare box plots and analyze measures of center and variability. They will also be given a set of three box plots and asked to identify and compare their measures of center and variablity. |
| Marshmallow Madness | This lesson allows students to have a hands-on experience collecting real-world data, creating graphical representations, and analyzing their data. Students will make predictions as to the outcome of the data and compare their predictions to the actual outcome. Students will create and analyze line plots, histograms, and box plots. |
| Digging the Plots | Students construct box plots and use the measure(s) of center and variability to make comparisons, interpret results, and draw conclusions about two populations. |
| A Walk Down the Lane | Students will collect data, and create box plots. Students will make predictions about which measurement best describes the spread and center of the data. Students will use this information to make predictions. |
| How Old are the Players? | For this lesson, students will research the ages of players on two basketball teams. They will find the five-number summary, the mean, and determine if there are outliers in the data set. Two box plots will be created and the measures of center and variation analyzed. |
| Who is the world's best ball player? | Students will compare sets of box and whisker plots to determine who is the better basketball player, Lebron James or Michael Jordan. |
| Centers, Spreads, and Outliers | The students will compare the effects of outliers on measures of center and spread within dot plots and box plots. |
| The Penny Lab | Students will design an investigation to collect and analyze data, determine results, write a justification and make a presentation using U.S. pennies.
Paired student teams will determine the mass of 50 U.S. pennies. Students will also collect other data from each penny such as minted year and observable appearance. Students will be expected to organize/represent their data into tables, histograms and other informational structures appropriate for reporting all data for each penny. Students will be expected to consider the data, determine trends, and research information in order to make a claim that explains trends in data from minted U.S. pennies.
Hopefully, student data reports will support the knowledge that the metallic composition of the penny has changed over the years. Different compositions can have significantly different masses. A sufficiently random selection of hundreds of pennies across the class should allow the students to discover trends in the data to suggest the years in which the composition changed. |
| Baking Soda and Vinegar: A statistical approach to a chemical reaction. | Students experiment with baking soda and vinegar and use statistics to determine which ratio of ingredients creates the most carbon dioxide. This hands-on activity applies the concepts of plot, center, and spread. |
| Homework or Play? | Students will be given data and then plot the data using a graphical method of choice (dot plot, bar graph, box plot, etc.) The students will work in groups and then analyze and summarize the data. |
| Lucky Number Seven | In "Lucky Number Seven", students will have fun generating individual data in this lesson introducing the creation of histograms. Working in pairs, students will roll number cubes, find the sum of each roll, and complete a chart. Through guided practice, students will learn how to organize the charted data and create a histogram. Supplemental independent practice is provided along with suggestions for formative and summative assessment. |
| Interpreting Box Plots | Students will analyze various real world scenario data sets and create, analyze, and interpret the components of the box plots. Students will use data from morning routines, track times, ages, etc. Lesson includes a PowerPoint, homework, and assessments. |
| Exploring Box plots | This lesson involves real-world data situations. Students will use the data to create, explore, and compare the key components of a box plot. |
| The Debate: Who is a Better Baller? | In this activity the students will use NBA statistics on Lebron James and Tim Duncan who were key players in the 2014 NBA Finals, to calculate, compare, and discuss mean, median, interquartile range, variance, and standard deviation. They will also construct and discuss box plots. |
| Got Homework? | Students will gather data to create dot plots, box plots, and histograms. They will examine each type of graph and compare the different representations. |
| Who's Better?--Using Data to Determine | This lesson is intended for use after students are able to construct data plots (histograms, line plots, box plots). Students are tasked with not only constructing data plots, but also matching data plots to data sets. In the summative assessment, students are given two data sets and asked to select which of three data plots (histogram, line plot, or box plot) would best be used to compare the data. After choosing and constructing their plot, students are then tasked with forming a conclusion based on the plots they have constructed. |
| Burgers to Smoothies. | Students will create double box plots to compare nutritional data about popular food choices. |
| Advantages and Disadvantages of Dot Plots, Histograms, and Box Plots | Students will compare the advantages and disadvantages of dot plots, histograms, and box plots. During this lesson, students will review the statistical process and learn the characteristics of a statistical question; whether it be numerical or categorical. Students will apply the information learned in a project that involves real-world issues and make an analysis based on the data collected. |
| Inferences | This lesson shows students how to conduct a survey and display their results. The lesson takes the students through:
- What is a statistical question?
- General population versus sample population.
- What is a hypothesis?
- What is a survey?
- How to make inferences.
|
| Box Plots | An introduction lesson on creating and interpreting box plots. |
| Statistically Speaking Part I: An Investigation of Statistical Questions and Data Distribution | This lesson is Part 1 of 2 and uses the inquiry-based learning method to help students recognize a statistical question as one that anticipates variability in the data. Through cooperative learning activities, students will learn how to analyze the data collected to answer a statistical question. Since this lesson focuses on math concepts related to identifying clusters, gaps, outliers, and the overall shape of a line plot, it will help students build a strong foundation for future concepts in the statistics and probability domain. Part 2 of this lesson is Resource ID #49091. |
| Be the Statistician | Students will utilize their knowledge of data and statistics to create a question, collect numerical data, and create a display of their data driven by its quantitative measures of center and variability; mean, median, mode, and range. |
| Best School for Kevin | In this Model Eliciting Activity, MEA, students will compare and analyze data, create histograms, and provide recommendations on the best school for a student new to the area.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx |
| Closest to the Pin! | Students will create and analyze real world data while representing the data visually and comparing to a larger sample size. |
| Hot, Hot, Hot! Earth Heating Up | Students will explore the concept of the uneven heating of Earth's surfaces by the Sun by collecting and analyzing data. Outside the classroom, students from several classes will record data points to be analyzed collectively to explore rates of heating related to time and material properties for air, water, and soil. Students will use mathematical techniques to help answer scientific questions. |
| Using Box Plots to Interpret Data | This lesson explores the creation of box plots to compare two data sets and draw inferences. |