Standard #: MA.6.GR.2.3

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.6.NSO.2.1
• MA.6.NSO.2.2
• MA.6.NSO.2.3
• MA.6.NSO.3.5
• MA.6.AR.1.1
• MA.6.AR.2.3

 

Terms from the K-12 Glossary

• Algorithm
• Cube
• Rectangular prism

 

Vertical Alignment

Previous Benchmarks

• MA.5.GR.3.3

Next Benchmarks

• MA.7.GR.2.3

 

Purpose and Instructional Strategies

Students in grade 5 found the volume of right rectangular prisms with whole-number edges. Students calculated the volume of right rectangular prisms (boxes) using whole-number edges with a unit cube of 1×1×1. In grade 6, students will use this understanding and apply it to rational-number edge lengths of rectangular prisms. In grade 7, students will find the volume of right circular cylinders. 

• Instruction includes exploring volume of the right rectangular prisms using fractional unit cubes.
  • For example, the right rectangular prism has edges of 1$\frac{\text{1}}{\text{4}}$ inches, 1 inch and 1$\frac{\text{1}}{\text{2}}$ inches. The volume can be found by recognizing that the unit cube would be $\frac{\text{1}}{\text{4}}$ inch of all edges, changing the dimensions to $\frac{\text{5}}{\text{4}}$ inches, $\frac{\text{4}}{\text{4}}$ inches and $\frac{\text{6}}{\text{4}}$ inches. The volume is the number of unit cubes making up the prism (5×4×6), which is 120 unit cubes each with the volume of $\frac{\text{1}}{\text{64}}$ = ($\frac{\text{1}}{\text{4}}$ × $\frac{\text{1}}{\text{4}}$ × $\frac{\text{1}}{\text{4}}$). This can also be expressed as ($\frac{\text{5}}{\text{4}}$ × $\frac{\text{6}}{\text{4}}$ × $\frac{\text{4}}{\text{4}}$) OR ($\frac{\text{120}}{\text{64}}$).
• “Know the formula” does not mean memorization of the formula. To “know” means to have an understanding of why the formula works and how the formula relates to the measure (volume) and the figure.
• Instruction includes measuring volume by filling rectangular prisms with blocks and looking at the relationship between the total volume and the area of the base. Through these experiences, students can derive the volume formula.
• When using rational numbers, instruction should stay within the same form. Students should not be penalized though if they convert from one form to another when performing operations.

o For example, if students are working with fractions, the side lengths will not include decimals. If students are working with decimals, the side lengths will not include fractions.

• Instruction includes using the formula of $V$ = $B$$h$ as well as the formula $V$ = $l$$w$$h$. Students should know when and how to use each formula and be able to apply the formulas to real-world contexts.
  • When given a problem such as “The standard size of a construction brick is 2$\frac{\text{1}}{\text{4}}$ inches by 8 inches by 3$\frac{\text{1}}{\text{2}}$ inches. Find the volume of one brick.” There are three measurements given. Therefore, the formula, $V$ = $l$$w$$h$, would be the most appropriate formula.
  • When given a problem such as “The floor of a cargo truck is 22$\frac{\text{1}}{\text{2}}$ square feet. What is the volume of the storage space in cubic feet if the truck is 7$\frac{\text{1}}{\text{5}}$ feet high?”, there are two measurements given with one being the area of a base. Therefore, the formula V = $B$$h$ would be the most appropriate formula.
• Instruction includes representing measurements for volume as cubic units, units cubed or units³.
• Problem types include having students measure lengths using a ruler to determine the area.

 

Common Misconceptions or Errors

• Students may invert the formulas for surface area and volume.
• Students incorrectly identify the units for volume. For example, use square inches to represent volume instead of cubic inches.

 

Strategies to Support Tiered Instruction

• Teacher reviews definitions of surface area and volume, and co-creates an anchor chart to display in the room explaining each. Providing flash cards or cue cards with the formulas will help students in place of anchor charts when they are outside the classroom area.
• Teacher explains the difference between two-dimensional and three-dimensional shapes. When working with two-dimensional shapes, we label in units², but when working with three-dimensional shapes, we label with units³.
• Teacher models the use of manipulatives and geometric software to review the concept of area and perimeter.
• Teacher breaks down formulas for area of a rectangle and volume of a rectangular prism to show when finding area, we are multiplying two sides, which is why we use units², but with the rectangular prism, we are multiplying three sides, so we use units³ to label.

 

Instructional Tasks

Instructional Task 1 (MTR.4.1, MTR.5.1)
Imagine that the prism pictured below is packed full of smaller identical prisms. The length of each edge of the small prisms is a unit fraction.

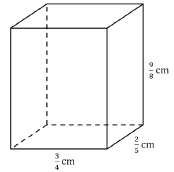
• Part A. Give the dimensions of the small prisms that can be used to pack the larger prism.
• Part B. How many of the small prisms would it take to completely fill the larger prism? Explain how you found your answer.
• Part C. Explain how the number of the small prisms needed to fill the larger prism is related to the volume of the large prism.

 

Instructional Items

Instructional Item 1
A right rectangular prism has a length of 4$\frac{\text{1}}{\text{2}}$ feet, a width of 6$\frac{\text{1}}{\text{2}}$ feet and a height of 8 feet. What is the volume of the prism?

Instructional Item 2
Alex has 64 cubes, with dimensions in feet (ft), like the one shown.
He uses all the cubes to fill a box shaped like a larger rectangular prism. There are no gaps between the cubes.

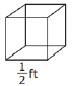
• Part A. What is the volume, in cubic feet, of the larger rectangular prism?
• Part B. What is a possible set of dimensions, in feet, of the larger rectangular prism?

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.