General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 4, students identified and generated equivalent fractions, and in grade 5, students represented the division of two whole numbers as a fraction. This was a foundation for ratio relationships relating parts to wholes. In grade 6, students work with ratios that can compare parts to whole or parts to parts. In grade 7, students use ratio comparisons in multi-step problems that may also involve percentages.- A ratio describes a multiplicative comparison that relates quantities within a given situation. Instruction emphasizes the understanding of the concept of a ratio and its similarities to a fraction and division.
- When working with ratios in context, the context should drive the form of the ratio.
- For example, there are 42 students on a school bus. 12 students are girls and the rest are boys. What is the ratio of girls to boys on the school bus? It is not necessary to simplify this ratio since the unsimplified ratio, 12 to 30, is more descriptive of the actual number of students on the bus.
- Allow student flexibility in accepting both simplified and non-simplified responses. This provides an opportunity for students to have discussions about why they have different responses and to connect various forms of a ratio to equivalent fractions (MTR.4.1).
- Instruction includes the use of manipulatives and models to represent ratios. Manipulatives and models include snap cubes, marbles, bar models, number lines or ratio tables to help visually represent the relationship. Students can also act out the ratio relationship in the classroom to help with visualization (MTR.2.1).
- Bar Models
The ratio of toy cars to toy airplanes in Andrew’s collection is 3:5.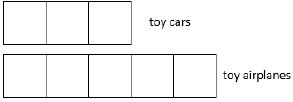
- Number Lines
The ratio of toy cars to toy airplanes in Andrew’s collection is 3:5.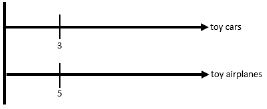
- Ratio Tables
The ratio of toy cars to toy airplanes in Andrew’s collection is 3:5.
- Bar Models
- Students should be able to write ratio relationships in all three forms: fraction, using “to”, or with a colon (:) between two numbers. They are not expected to write it in all three forms for every problem.
- Instruction includes writing the ratio and interpreting its meaning in the provided real-world context (MTR.5.1, MTR.7.1).
- Ratios can compare quantities of any kind, including counts of people or objects, measurements of length, weight and time.
- Problem types include providing real-world context with written descriptions, charts and tables.
- In some cases, the context of a problem determines a specific ratio, as well as the order in which a ratio is written.
- For example, there are 2 blue marbles and 5 red marbles. Write the ratio of red marbles to blue marbles.
- Acceptable responses: 5:2, 5 to 2 or .
- For example, there are 2 blue marbles and 5 red marbles. Write the ratio of red marbles to blue marbles.
- In other cases, the context of a problem does not determine the order in which a ratio is written, and it may involve more than one ratio.
- For example, there are 2 blue marbles and 5 red marbles. Write a ratio relationship.
- Acceptable responses: 2:5, 5:2, 2 to 7, 7 to 2, or .
- For example, there are 2 blue marbles and 5 red marbles. Write a ratio relationship.
Common Misconceptions or Errors
- Students may incorrectly reverse the order of a ratio when a question does specify the order. To address this misconception, students can color code or write the order of the description before assigning the numbers to the ratio.
- Students may not recognize simplified forms of ratios. It is not required that students determine the simplified version of a ratio, but when comparing the ratios with other students and seeing different numbers, students should become more adept at seeing both ratios as representing the same relationship. The student should be reminded of the connection to equivalent fractions.
Strategies to Support Tiered Instruction
- Instruction includes using colored pencils to identify the units in each corresponding portion of a ratio and identifying the units before writing the numerical values.
- For example, Leslie and Sabrina are both running for class president. If for every two votes Leslie receives, Sabrina receives five, describe the relationship between the number of votes Leslie receives to the number of votes Sabrina receives as a ratio.Leslie’s votes to Sabrina’s votes
2 to 5, or 2:5, or
- For example, Leslie and Sabrina are both running for class president. If for every two votes Leslie receives, Sabrina receives five, describe the relationship between the number of votes Leslie receives to the number of votes Sabrina receives as a ratio.
- Instruction includes the use of two different counters to represent the provided ratio to allow for students to explore equivalent ratios by adding additional sets of counters or by dividing the existing counters into equal groups.
- Teacher reminds students of the connection between ratios and equivalent fractions.
Instructional Tasks
Instructional Task 1 (MTR.4.1, MTR.7.1)To make the color purple, Jamal’s art teacher instructed him to mix equal parts of red paint
and blue paint. To make a different shade of purple, the ratio of red paint to blue paint is 2:1. What does the ratio 2:1 mean? Would a ratio of 1:2 make the same color? Why or why not?
Instructional Task 2 (MTR.4.1)
Mr. Keen, a band teacher, wanted to know if certain types of instruments are more appealing to one grade level or another. So, he conducted a survey of his students’ preferences. The results are compiled in the chart below.
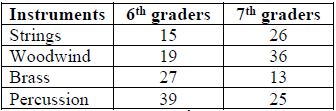
- Part A. What is the ratio of the number of 6th graders preferring woodwind instruments to the number of 7th graders preferring woodwind instruments?
- Part B. What is the ratio of the number of 7th graders preferring percussion instruments to the total number of 7th graders surveyed?
- Part C. What does the ratio of 27:40 represent? Does the ratio of 40 to 27 represent the same concept? Why or why not?
Instructional Items
Instructional Item 1Ana and Robbie both stayed after school for help on their math homework. Ana stayed for 15 minutes and Robbie stayed for 50 minutes. Write a ratio to represent the relationships between the time that Ana stayed for help and the time that Robbie stayed for help.
Instructional Item 2
Leslie and Sabrina are both running for class president. If for every two votes Leslie receives, Sabrina receives five, describe the relationship between the number of votes Leslie receives to the number of votes Sabrina receives as a ratio.
Instructional Item 3
Miss Williams asked her class if they prefer doing their homework before school or after school. If the ratio of students who prefer doing homework before school to students who prefer doing homework after school is , what does the ratio represent? Explain.

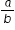 , a to b, or a:b where b ≠ 0.
, a to b, or a:b where b ≠ 0.