Standard #: MA.6.AR.2.1

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.6.NSO.4.1
• MA.6.NSO.4.2
• MA.6.AR.1.2
• MA.6.AR.1.3

 

Terms from the K-12 Glossary

• Coefficient
• Distributive Property
• Equation
• Integer

 

Vertical Alignment

Previous Benchmarks

• MA.5.AR.2.2
• MA.5.AR.2.3

Next Benchmarks

• MA.7.AR.2.1
• MA.7.AR.2.2

 

Purpose and Instructional Strategies

In grade 5, students evaluated numerical expressions as well as simplified numerical expressions on both sides of an equation to determine if the equation was true or false. In grade 6, the skills are extended to evaluating expressions where students must substitute the given value of a variable. Students are also expected to use substitution with multiple variables within algebraic equations and inequalities to determine which of the given values make the mathematical statement true and which make it false. The substituted values in grade 6 are limited to integers. This skill extends into grade 7 where students learn to solve two-step equations and one-step inequalities to determine their rational number solutions.

• Instruction focuses on the understanding that solving an equation or inequality is a process of answering the question:
  • Which values from a specified set, if any, make the equation or inequality true?
• Instruction emphasizes the understanding of defining an algebraic inequality. Students should have practice with inequalities in the form of $x$ > $a$, $x$ < $a$, $x$ ≥$\mathrm{ a}$ and $x$ ≤$\mathrm{ a}$. Students should explore how “is greater than or equal to” and “is strictly greater than” are similar and different as well as “is less than or equal to” and “is strictly less than.” Students should use academic language when describing the algebraic inequality (MTR.4.1).
• Students should understand a variable can represent an unknown number or, depending on the context, any value in a specified set.
• Instruction includes using set notation to list numbers but not writing solutions in set notation as well as equations where the same variable is in more than one term or on both sides of the equation or inequality. Set notation does not require descending or ascending order.
  • Set notation: {−3, 0, 4, 11} or {5, −3, 2, 0, 13}.
• For this benchmark, students are not expected to perform operations with negative rational numbers.

 

Common Misconceptions or Errors

• Some students may incorrectly believe only one value can make an inequality true. Inequalities describe a relationship between expressions that more than one value can satisfy.
• If more than one operation is present, students may incorrectly think there is always only one way to accurately evaluate it when there may be more than one accurate method.
  • For example, if students are asked to determine the truth value of $x$ = 8 given the equation 2$x$ −3($x$ −4) = 4, students could accurately solve using order of operations and properties of operations in more than one way.

 

Strategies to Support Tiered Instruction

• Instruction includes the use of pictorial representations, tape diagrams, or algebra tiles to represent the equation or inequality then replacing the variables with the possible solutions to test for the equation or inequality to be true.
  • For example, the following representations can be used to determine which of the values, 4, 5 or 6, make the equation 4$x$ +5 = 25 true.
4$x$ +5 = 25:


4$x$ +5 ≠ 25, when $x$ = 4


4$x$ +5 = 25, when $x$ = 5


4$x$ +5 ≠ 25, when $x$ = 6


• Teacher provides instruction with a simple inequality statement and its graph, and then has students use substitution and the number line to test for possible solutions. Gradually remove the support of the number line and transition students to using only substitution to test for possible values to make the given inequalities true.

 

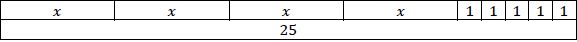
Instructional Tasks

Instructional Task 1 (MTR.4.1)

• Explain what it means for a number to be a solution to an equation. Explain what it means for a number to be a solution to an inequality.

Instructional Task 2 (MTR.3.1, MTR.4.1, MTR.5.1) 

• Provide students with a set of integer values. 
  • Part A. Choose one of the integer values and create an equation that would make a true statement with your selected value.
  • Part B. Compare your equation with someone who chose the same value and a different value. What do you notice?
  • Part C. Choose two of the integer values and create an inequality that would make a true statement with your selected values. Create another inequality that would make a true statement with one of your selected values but not the other.
  • Part D. Compare your inequality with someone who chose the same values and someone who chose different values. What do you notice?
• Which of the following values are solutions to the inequality 6$a$ +2 ≤ $a$ − 23?
  a. −5
  b. $\frac{\text{21}}{\text{5}}$
  c. −25
  d. 5
  e. 4.2
  f. −$\frac{\text{25}}{\text{7}}$

 

Instructional Items

Instructional Item 1

• Which of the following values makes the equation 3$x$ +8 = 14 true?
  a. −2
  b. 2
  c. 3
  d. 6

Instructional Item 2

• Which of the following values make the inequality 4$x$ +5 > 25 true?
  a. −3
  b. 4
  c. 5
  d. 6
  e. 12

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.