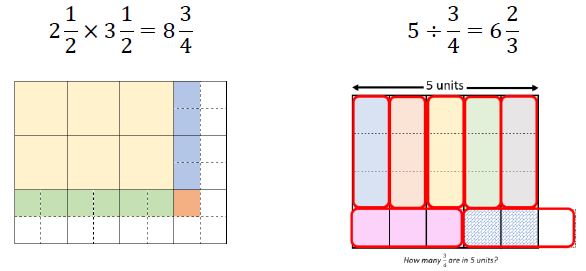
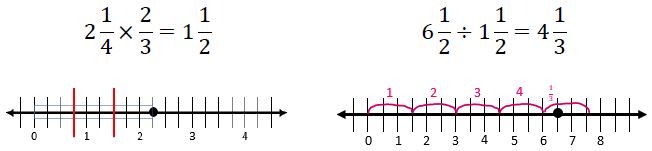
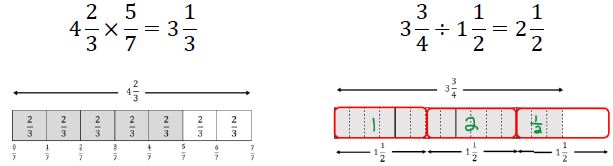
Extend previous understanding of multiplication and division to compute products and quotients of positive fractions by positive fractions, including mixed numbers, with procedural fluency.
Instruction focuses on making connections between visual models, the relationship between multiplication and division, reciprocals and algorithms.
| Name |
Description |
| Who's Your Match? | Students will be able to match a 3-D shape with its net, then using the net, they will find the surface area of the shape. They will then be able to apply this knowledge to solve real world application problems, finishing up with a design contest. |
| Extending the Distributive Property | In this lesson, students will build upon their arithmetic experiences with the distributive property to equate algebraic expressions through a series of questions related to real world situations and the use of manipulatives. Activities include the use of Algebra Tiles for moving the concrete learner to the abstract level and the use of matching cards.
This is an introductory lesson that only includes producing equivalent expressions such as 3(2 + x) = 6 + 3x. |
| Using Nets to Find the Surface Area of Pyramids | In this lesson, students will explore and apply the use of nets to find the surface area of pyramids. |
| Wrapping Up Geometry (Lesson 1 of 2) | This lesson is the first of two in a unit on surface area. This lesson provides a foundation for understanding the concept of surface area by introducing nets of right rectangular prisms. |
| Aquarium Splash | Students explore how the formulas for surface area and volume were derived and apply this knowledge to solve problems. Students will be presented with a problem-solving task that incorporates finding the surface area and volume when designing an aquarium. |
| Dividing Fractions: Increasing Procedural Skill | This lesson helps students develop procedural skills in dividing fractions. During this lesson students will discuss prior knowledge of the concept of dividing fractions and will solve problems independently and in pairs using the standard algorithm. The lesson also incorporates music and poster-making to reinforce the learning objective. This lesson was originally designed for a 6th-grade Intensive Math class and should only be used following lessons where students have developed a solid conceptual understanding of dividing fractions. This lesson may take up to 3 days depending on how much practice and extra activities your students require. |
| Let's Understand Multiplication of Positive and Negative Numbers | This lesson provides teachers with a way to show students why multiplying negative numbers results in a positive answer. The lesson starts with a review of decomposition, the distributive property, and finding missing addends. Then, with teacher guidance, groups of students apply these skills in a systematic way to apply properties of operations to discover the rules governing the signs of products for positive and negative factors and to multiply positive and negative numbers in mathematical and real-world problems. Finally, students independently demonstrate mastery of the lesson objectives by completing an independent practice assessment. |
| Netty People and Pets | Students will learn what the "net" of a three-dimensional figure is, draw nets of right-rectangular prisms and right-rectangular prisms, accurately calculate the surface area of nets, and put nets together to create an original “person” or “pet.” |
| What's on the Surface? | In this activity, students will work in groups to evaluate the measurements of shapes that form three-dimensional composite shapes to compute the surface area. |
| Can You Find the Relationship? | In this lesson students will first define in their own words what the greatest common factor (GCF) and least common multiple (LCM) mean. They will take this understanding and apply it to solving GCF and LCM word problems. Students will then illustrate their understanding by creating posters based on their word problems. There are examples of different types of methods, online games, a rubric, and a power point to summarize this two-day lesson. |
| How Many Rubik's Cubes Can You Pack? | This two-day lesson uses a hands-on problem-solving approach to find the volume of a right rectangular prism with positive rational number edge lengths. Students first design boxes and fill with Rubik's Cubes. They create a formula from the patterns they find. Using cubes with fractional edges requires students to apply fractional units to their formulas. |
| Who's Your Match? | Students will be able to match a 3-D shape with its net, then using the net, they will find the surface area of the shape. They will then be able to apply this knowledge to solve real world application problems, finishing up with a design contest. |
| Fill to Believe! | In this lesson, students work cooperatively to find the volume of a right rectangular prisms, using whole and fraction units of measurement, using the volume formula, and using manipulatives to count the number of units necessary to fill the prisms, and compare it with the formula results. |
| Can you say that another way? | Students will model how to express an addition problem using the distributive property. |
| Surface Area of Prisms and Pyramids | In this lesson students will find the surface area of three-dimensional figures. Students will use nets to calculate the surface area of right rectangular prisms and right rectangular pyramids. |
| The Price is Right | In this activity the students will apply their knowledge of mathematical calculations to solve a real-world problem. They will analyze a collection of shipping boxes to determine which box will ship the most for the $100 allowed. |
| How Much Paint Will It Take? | This is a guided inquiry lesson to help students gain greater understanding of the relationship between 2-dimensional and 3-dimensional shapes. Students create right rectangular prisms and problem-solve how to find the flat 2-dimensional surface area. Students are asked to figure out how many party favors (prisms) can be painted with a quart of glow-in-the-dark paint. |
| Box It Up, Wrap It Up (Surface Area of Rectangular Prisms) | In this introductory lesson to surface area, students will make connections between area of two-dimensional figures and calculating the surface area of rectangular prisms using nets, within the context of wrapping birthday presents! Math is Fun :) |
| You Can Never Have Too Many Shoes! | This lesson teaches Least Common Multiples. |
| How Many Small Boxes? | In this lesson students will extend their knowledge of volume from using whole numbers to using fractional units. Students will work with adding, multiplying, and dividing fractions to find the volume of right rectangular prisms, as well as, determining the number of fractional unit cubes in a rectangular prism. |
| Finding the Greatest Crush Factor | This lesson uses a real-life approach to exploring the use of Greatest Common Factors (GCF). The students will utilize math practice standards as they analyze math solutions and explain their own solutions. |
| Factoring out the Greatest | This lesson teaches students how to find the GCF and LCM by factoring. This is a different method than is normally seen in textbooks. This method easily leads to solving GCF word problems and using the distributive property to express a sum of two whole numbers. |
| Dividing Fractions | In this lesson students will explore the different methods available for dividing fractions through a student-based investigation. The teacher will facilitate the discussion, but the students will discover the different methods on their own or with a partner as they work through the different steps. |
| Wrapping Up Geometry (Lesson 2 of 2) | This lesson is 2 of 2 and is primarily formative in nature, but includes a summative assessment for students to take during the following class period.
During the lesson, students will be reviewing for their assessment on the surface area formula for a right rectangular prism.
|
| Dividing Fractions (Part 1) - Tackling Word Problems | This lesson allows the students to explore the foundation for dividing fractions as well as correctly solving word problems involving division of fractions. It includes the use of the Philosophical Chairs activity and numerical solutions. Group activities are included to foster cooperative learning. |
| Multiplying a Fraction by a Fraction | Students will multiply a fraction times a fraction. The students will section off a square through rows and columns that will represent the strategy of multiplying numerators and then denominators.
|
| Dividing by Fractions Discovery | This lesson allows students to derive an algorithm for dividing fractions using visual fraction models and equations to represent the problem. |
| Sweet Surface Area | In this lesson, students will explore the relationship between volume and surface area through real-world problem solving. They will work with a partner as they are tasked with finding the least expensive packaging (smallest surface area) for a given number of caramels (volume). Students will justify their packaging strategy in a group discussion. |
| Modeling Fraction Multiplication | This lesson involves students modeling fraction multiplication with rectangular arrays in order to discover the rule for multiplication of fractions. |
| Formula Detective: Finding the Surface Area of a 3D Figure | This lesson allows students to derive the formulas for 3D figures by having them build models for nets. |
| All wrapped up in surface area fun! | This lesson allows a hands-on approach for students to use real-life problem-solving. Students will apply their measurement skills to the concept of surface area. This lesson provides opportunities for students to work cooperatively with others as a team. |
| Let's Translate!! | Students will translate verbal phrases into algebraic expressions. Students are given practice in writing expressions that record operations with numbers and variables. Special attention is given to writing operations in the correct order. Class work and homework worksheets are provided with answer keys for each. |
| Name |
Description |
| Running to School, Variation 2 | Students are asked to solve a distance problem involving fractions. |
| Making Hot Cocoa, Variation 1 | Students are asked to solve a fraction division problem using both a visual model and the standard algorithm within a real-world context. |
| Making Hot Cocoa, Variation 2 | Students are asked a series of questions involving a fraction and a whole number within the context of a recipe. Students are asked to solve a problem using both a visual model and the standard algorithm. |
| Running to School, Variation 3 | Students are asked to solve a distance problem involving fractions. The purpose of this task is to help students extend their understanding of division of whole numbers to division of fractions, and given the simple numbers used, it is most appropriate for students just learning about fraction division because it lends itself easily to a pictorial solution. |
| Traffic Jam | Students are asked to use fractions to determine how many hours it will take a car to travel a given distance. |
| Video Game Credits | Students are asked to use fractions to determine how long a video game can be played. |
| Baking Cookies | The purpose of this task is to help students get a better understanding of multiplying and dividing using fractions. |
| Cup of Rice | The purpose of this task is to help give students a better understanding of multiplying and dividing fractions. |
| Dan’s Division Strategy | The purpose of this task is to help students explore the meaning of fraction division and to connect it to what they know about whole-number division. Students are asked to explain why the quotient of two fractions with common denominators is equal to the quotient of the numerators of those fractions. |
| Drinking Juice, Variation 2 | This task builds on a fifth grade fraction multiplication task, "Drinking Juice." This task uses the identical context, but asks the corresponding "Number of Groups Unknown" division problem. See "Drinking Juice, Variation 3" for the "Group Size Unknown" version. |
| Drinking Juice, Variation 3 | Students are asked to solve a fraction division problem using a visual model and the standard algorithm. |
| How Many _______ Are In. . . ? | This instructional task requires that the students model each problem with some type of fractions manipulatives or drawings. This could be pattern blocks, student or teacher-made fraction strips, or commercially produced fraction pieces. At a minimum, students should draw pictures of each. The above problems are meant to be a progression which require more sophisticated understandings of the meaning of fractions as students progress through them. |
| How Many Containers in One Cup / Cups in One Container? | The purpose of this problem is to help students deepen their understanding of the meaning of fractions and fraction division and to see that they get the same answer using standard algorithm as they do just reasoning through the problem. These two fraction division tasks use the same context and ask "How much in one group?" but require students to divide the fractions in the opposite order. Students struggle to understand which order one should divide in a fraction division context, and these two tasks give them an opportunity to think carefully about the meaning of fraction division. |
| Name |
Description |
| Running to School, Variation 2: | Students are asked to solve a distance problem involving fractions. |
| Making Hot Cocoa, Variation 1: | Students are asked to solve a fraction division problem using both a visual model and the standard algorithm within a real-world context. |
| Making Hot Cocoa, Variation 2: | Students are asked a series of questions involving a fraction and a whole number within the context of a recipe. Students are asked to solve a problem using both a visual model and the standard algorithm. |
| Running to School, Variation 3: | Students are asked to solve a distance problem involving fractions. The purpose of this task is to help students extend their understanding of division of whole numbers to division of fractions, and given the simple numbers used, it is most appropriate for students just learning about fraction division because it lends itself easily to a pictorial solution. |
| Traffic Jam: | Students are asked to use fractions to determine how many hours it will take a car to travel a given distance. |
| Video Game Credits: | Students are asked to use fractions to determine how long a video game can be played. |
| Dan’s Division Strategy: | The purpose of this task is to help students explore the meaning of fraction division and to connect it to what they know about whole-number division. Students are asked to explain why the quotient of two fractions with common denominators is equal to the quotient of the numerators of those fractions. |
| Drinking Juice, Variation 2: | This task builds on a fifth grade fraction multiplication task, "Drinking Juice." This task uses the identical context, but asks the corresponding "Number of Groups Unknown" division problem. See "Drinking Juice, Variation 3" for the "Group Size Unknown" version. |
| Drinking Juice, Variation 3: | Students are asked to solve a fraction division problem using a visual model and the standard algorithm. |
| How Many _______ Are In. . . ?: | This instructional task requires that the students model each problem with some type of fractions manipulatives or drawings. This could be pattern blocks, student or teacher-made fraction strips, or commercially produced fraction pieces. At a minimum, students should draw pictures of each. The above problems are meant to be a progression which require more sophisticated understandings of the meaning of fractions as students progress through them. |
| Name |
Description |
| Running to School, Variation 2: | Students are asked to solve a distance problem involving fractions. |
| Making Hot Cocoa, Variation 1: | Students are asked to solve a fraction division problem using both a visual model and the standard algorithm within a real-world context. |
| Making Hot Cocoa, Variation 2: | Students are asked a series of questions involving a fraction and a whole number within the context of a recipe. Students are asked to solve a problem using both a visual model and the standard algorithm. |
| Running to School, Variation 3: | Students are asked to solve a distance problem involving fractions. The purpose of this task is to help students extend their understanding of division of whole numbers to division of fractions, and given the simple numbers used, it is most appropriate for students just learning about fraction division because it lends itself easily to a pictorial solution. |
| Traffic Jam: | Students are asked to use fractions to determine how many hours it will take a car to travel a given distance. |
| Video Game Credits: | Students are asked to use fractions to determine how long a video game can be played. |
| Baking Cookies: | The purpose of this task is to help students get a better understanding of multiplying and dividing using fractions. |
| Dan’s Division Strategy: | The purpose of this task is to help students explore the meaning of fraction division and to connect it to what they know about whole-number division. Students are asked to explain why the quotient of two fractions with common denominators is equal to the quotient of the numerators of those fractions. |
| Drinking Juice, Variation 2: | This task builds on a fifth grade fraction multiplication task, "Drinking Juice." This task uses the identical context, but asks the corresponding "Number of Groups Unknown" division problem. See "Drinking Juice, Variation 3" for the "Group Size Unknown" version. |
| Drinking Juice, Variation 3: | Students are asked to solve a fraction division problem using a visual model and the standard algorithm. |
| How Many _______ Are In. . . ?: | This instructional task requires that the students model each problem with some type of fractions manipulatives or drawings. This could be pattern blocks, student or teacher-made fraction strips, or commercially produced fraction pieces. At a minimum, students should draw pictures of each. The above problems are meant to be a progression which require more sophisticated understandings of the meaning of fractions as students progress through them. |