General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 5
Strand: Geometric Reasoning
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Coordinate Plane (first quadrant)
- Origin
- x-axis
- y-axis
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to extend their thinking from grade 4 (MA.4.NSO.1.3) about horizontal and vertical number lines to plot and label whole number ordered pairs on a coordinate plane. In addition, students will make a connection between a two- column table and the ordered pairs represented on the coordinate plane. In grade 6 (MA.6.GR.1.1), students plot rational number pairs in all four quadrants of the coordinate plane.- During instruction, teachers should relate the coordinate plane as the intersection of two axes – a horizontal number line called the ??-axis and a vertical number line called the y- axis. The number lines that form the axes are perpendicular and meet at the origin, labeled by the ordered pair (0, 0) (MTR.5.1).
- When students learn to plot ordered pairs represented in a two-column table, they should understand that the ordered pair (x, y) represents how far to travel from the origin along the x- and y-axes.
- For example, students should understand that in the ordered pair (2, 4), the point travels along the x-axis 2 whole units to the right, and then vertically (parallel to the y-axis) 4 units up (MTR.5.1).
Common Misconceptions or Errors
- Students can confuse the x- and y-values in an ordered pair and move vertically along the y-axis before moving horizontally along the x-axis.
- For example, they may mean to plot and label the ordered pair (2, 4), but plot and label (4, 2) instead. To assist students with this misconception, have students practice with creating directions for their student peers to follow to allow them to gain a better understanding of the direction and distance on the coordinate plane.
- Some students may not understand what an x- or y-coordinate value of 0 represents. During instruction, students should justify why ordered pairs with a 0 will plot on the x- axis or y-axis.
Strategies to Support Tiered Instruction
- Instruction includes the teacher providing coordinate points to graph in quadrant 1 of the coordinate plane along with two small objects. The students explain how they move the object along the x-axis and then up the y-axis to the location provided. The teacher then provides the points reversed to graph and has students explain the difference in how they move the second object compared to the first.
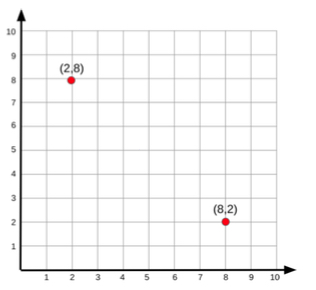
- For example, the teacher provides students with a coordinate plane like the one shown below. The teacher provides a set of coordinate points such as (8,2). Students take turns moving an object, such as a two-colored counter, and explain the location of the point using the x- and y-axis in their explanation. The teacher then provides the points in reverse, (2,8). The next student will move a second object and explain the location of the point as well as the difference between the two locations.
- Instruction includes the teacher providing a set of cards that have coordinate points on them, some with 0 as the location on the x-axis, some with 0 as the location on the y- axis, others with no 0 in the coordinates. Students sort the cards into three categories: points located on the x-axis, points located on the y-axis and neither. Students will justify their reasoning by explaining how the 0, or lack of a 0, in each set of points helped them.
- For example, the teacher provides cards with the following points on them: (2,5), (0,8), (3,0), (2,0), (1,9), (0,4), (6,0), (7,2), (9,0), (0,5) Students sort the points into three categories as shown below.
- Instruction includes the teacher creating a giant coordinate plane on the floor with painters' tape or outside with sidewalk chalk. The teacher or a student will then create directions for their peers to follow. The teacher or student will provide a set of coordinate points, including those with 0 as the x- or y-coordinate. Another student will physically move to the location, describing as they move, which axis they are moving on and counting the spaces until they reach their final location.
- For example, the teacher or a student tells a student to move to the location of (4,6) on the coordinate plane. The student says, “I begin at the origin which is (0,0) and move 1, 2, 3, 4 spaces to the right on the x-axis. I then move 1, 2, 3, 4, 5, 6 spaces up on the y-axis to my final location of (4,6).”
- For example: The teacher provides a student with the location (5,0). The student will move along the x-axis 5 spaces and stop. The teacher provides another student with the location (0,5). That student moves up the y-axis 5 spaces and stop. The teacher will then have the students explain how their location ended up on the x- or y-axis as well as the relationship between those located on the y-axis and those located on the y-axis.
Instructional Tasks
Instructional Task 1 (MTR.3.1)
Part A. A point has coordinates (3, 5). If you were to graph this point on a coordinate plane, what does the 3 tell you to do?Part B. Consider the same point with coordinates (3, 5). What does the 5 tell you to do?
Instructional Items
Instructional Item 1
What ordered pair represents the origin of a coordinate plane?- a. (0, 0)
- b. (1, 0)
- c. (0, 1)
- d. (1, 1)
Instructional Item 2
A point has coordinates (1, 6). If you were to plot this point on a coordinate plane, what does the 1 tell you to do?- a. From the origin, move along the x-axis 1 unit up.
- b. From the origin, move along the y-axis 1 unit up.
- c. From the origin, move along the x-axis 1 unit right.
- d. From the origin, move along the y-axis 1 unit right.
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.