Standard #: MA.5.GR.3.2


This document was generated on CPALMS - www.cpalms.org



Find the volume of a right rectangular prism with whole-number side lengths using a visual model and a formula.


Clarifications


Clarification 1: Instruction includes finding the volume of right rectangular prisms by packing the figure with unit cubes, using a visual model or applying a multiplication formula.

Clarification 2: Right rectangular prisms cannot exceed two-digit edge lengths and responses include the appropriate units in word form.



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 5
Strand: Geometric Reasoning
Standard: Solve problems involving the volume of right rectangular prisms.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Rectangular Prism

 

Vertical Alignment

Previous Benchmarks

 

Next Benchmarks

 

Purpose and Instructional Strategies

  • The purpose of this benchmark is for students to make connections between packing a right rectangular prism with unit cubes to determine its volume and developing and applying a multiplication formula to calculate it more efficiently. Students have developed experience with area since grade 3 (MA.3.GR.2.2). For volume, side lengths are limited to whole numbers in grade 5, and problems extend to fraction and decimal side lengths in grade 6 (MA.6.GR.2.3). 
  • Instruction should make connections between the exploration expected of MA.5.GR.3.1 and what is happening mathematically when calculating volume (MTR.2.1). 
  • Instruction should begin by connecting the measurement of a right rectangular prism to the calculation of a rectangle’s area. The bottom layer of the prism is packed with a number of rows with a number of cubes in each, like area of a rectangle is calculated with unit squares. From there, the third dimension (height) of the prism is calculated by the number of layers stacked atop one another. 
  • Having students explore how volume is calculated helps students see the patterns and develop a multiplication formula that will help them make sense of the two most common volume formulas, V = B × h (where B represents the area of the rectangular prism’s base) and V = l × w × h. If students understand conceptually what the formulas mean, they are more likely to use them effectively and efficiently (MTR.5.1). 
  • When students use a multiplication formula, it is important for them to see that it is a matter of choice which dimensions of rectangular prisms are named length, width and height. This will help students understand that when calculating the volume of a rectangular prism, the three dimensions are multiplied together and that the order of factors does not matter (commutative property of multiplication).

 

Common Misconceptions or Errors

  • Students may confuse the difference between b in the area formula A= b X h and B in the volume formula V = B × h. When building understanding of the volume formula for right rectangular prisms, teachers and students should include a visual model to justify their calculations. 
  • Students may make computational errors when calculating volume. Encourage them to estimate reasonable solutions before calculating and justify their solutions after. Instruction can also encourage students to find efficient ways to use the formula.
    • For example, when calculating the volume of a rectangular prism using the formula V = 45 × 12 × 2, students may find calculating easier if they multiply 45 × 2 (90) first, instead of 45 × 12. During class discussions, teachers should encourage students to share their strategies so they can build efficiency.

 

Strategies to Support Tiered Instruction

  • Instruction includes differentiating between base in the area formula, Area = b × h and base in the volume formula Volume = B × h. Teacher provides students with models of two-dimensional figures, and three-dimensional figures, and has them identify which formula they will use and what the base in each image is. 
    • For example, the students highlight the lines included in the base measurement for each figure. Then, they use the base to calculate the area or volume. The teacher provides students with a set of models like the one shown below asking which image they would use the area formula for and which image they would use the volume formula for. Students then highlight the measurements used for the base in the formula. For the first figure, students would use volume and the formula B × h with B = 16 × 4. For the second figure, students would find area and use the formula b × h with b = 16. 
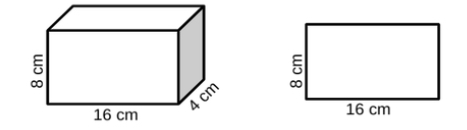
two-dimensional figures, and three-dimensional figure
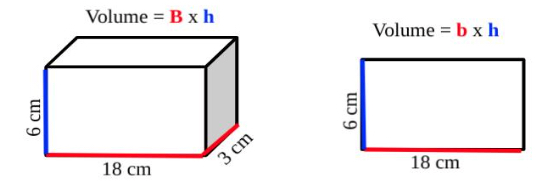
  • Instruction includes providing models of two-dimensional and three-dimensional figures with the area and volume formula labeled and color-coded with the measurements. 
    • For example, the teacher provides students with the following set of visual models and has students explain the difference in the base measurement in each formula. Students calculate the area or volume of each figure using the formula.
 two-dimensional and three-dimensional figure with the area and volume formula labeled and color-coded with the measurements
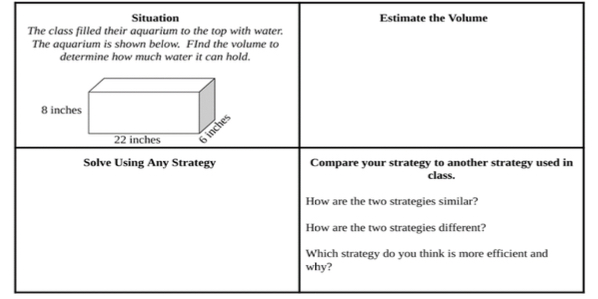
  • Instruction includes providing a graphic organizer that requires students to estimate the volume of real-world examples provided and then solve using any strategy they would like. 
  • For example, the teacher provides students with a graphic organizer similar to the one shown below. Students use it to find the volume of the given example and then compare their strategy to others. 
a graphic organizer
  • Instruction includes finding efficient ways to use the formula. 
    • For example, when calculating the volume of a rectangular prism using the formula V = 45 × 12 × 2, students may find calculating easier if they multiply 45 × 2 (which equals 90) first, instead of 45 × 12. During class discussions, teachers should encourage students to share their strategies so they can build efficiency. 
  • Instruction includes providing worked examples of volume and having students determine which strategy is the better strategy to use and why. 
    • For example, the teacher provides students with the following image and two examples of how students solved for volume. Student A solved the area of the base first using the Distributive Property to help with the multiplication. Student B used the Associative Property of Multiplication and multiplied 20 × 5 first. Students discuss both strategies and explain which would be easier and why.
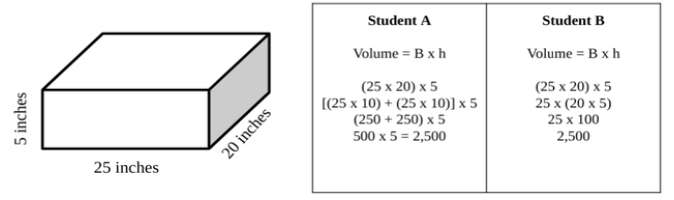
worked examples of volume

 

Instructional Tasks

Instructional Task 1 (MTR.2.1) 

The Great Graham Cracker Company is looking for a new package design for next year’s boxes. The boxes must be a right rectangular prism and measure 144 cubic centimeters. 
  • Part A. What are three package designs the company could use? Draw models and write equations to show their volumes. 
  • Part B. Dr. Cruz, the company’s founder, wants the height of the package to be exactly 8 centimeters. What are two package designs that the company can use? Draw models and write equations to show their volumes.

 

Instructional Items

Instructional Item 1 

Which of the following equations can be used to calculate the volume of the rectangular prism below?

rectangle prism

  • a. V=96×15 
  • b. V=15×8×12 
  • c. V=15×20 
  • d. V=27×8 
  • e. V=23×12 


Instructional Item 2 

A bedroom shaped like a rectangular prism is 15 feet wide, 32 feet long and measures 10 feet from the floor to the ceiling. What is the volume of the room? 
  • a. 57 cubic ft. 
  • b. 150 cubic ft. 
  • c. 4,500 cubic ft. 
  • d. 4,800 cubic ft. 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.




Related Courses

Course Number1111 Course Title222
5012070: Grade Five Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7712060: Access Mathematics Grade 5 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012065: Grade 4 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 and beyond (current))
5012015: Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.5.GR.3.AP.2 Find the volume of a right rectangular prism with whole-number side lengths by counting unit cubes. Explore that the volume is the same as what would be found by multiplying the edge lengths.


Related Resources

Formative Assessments

Name Description
Measuring Volume

Students are asked to determine the volume of a rectangular prism by using both a formula and counting cubic units.

Volume Two Ways

Students are asked to compare different strategies for finding the volume of a rectangular prism.

Find the Volume

Students are asked to count unit cubes to determine the volume of a right rectangular prism.

Determining and Interpreting Volume

Students are asked to determine the volumes of two right rectangular prisms given the dimensions of one and the base area and height of the other.

Lesson Plans

Name Description
Survive or Die

In this technology-rich lesson, students will design a habitat in which a plant or animal can survive. Students will focus on the adaptations that allow certain plants and animals to live in specific habitats.

Building Apartments: Connecting Volume of Centimeter Cubes to the Formula V = B x h

Students will build "apartments" with centimeter cubes by packing boxes (template included).  In addition, they will use centimeter cubes to build a variety of rectangular prisms and record the area of the base (B) and height (h) on a worksheet.  They will use that information to complete the volume formula, V = B x h.  Students will think about how the volume changes as the height and base of rectangular prisms change.

Lunchbox Volume

This lesson focuses on the application of volume knowledge.  Students will need to add the volumes of individual right rectangular prisms to find total volumes.

Volumize Your Brain To Its Capacity

Students will be able to apply and understand the meaning of volume with shoe boxes and cereal boxes. 

Getting the Top Mini-Fridge not a Small Deal

In this MEA, students will create a procedure to rank five mini-refrigerators to determine which one should be purchased for the school by the PTA based on size, type, features, energy usage, and cost.  In the process, students will solve real-world problems involving the multiplication of multi-digit numbers with decimals to the hundredths, including using money.  Students will also determine the volume of a rectangular prism using a formula.

MEA Bait Shop Baffle

Students will first review rectangular prisms and the formula for finding the volume of rectangular prisms. After students have determined the volume of a given set of rectangular prisms (aquariums), the students will use that information to help Seymour Phish in determining which aquarium he should purchase for his minnows.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

Volume, Mass, and Density Boxes

This activity was designed for blind learners, but all types of learners can utilize it to investigate volume, mass, and density. The learner will create several boxes with different materials in each. They will then compare the sizes and masses and do the math to figure the densities. Educators could also create a data collection chart for this activity.

Volume: Let's Be Efficient

This lesson provides a hands-on approach to develop the formula for finding the volume of a right rectangular prism. Students will apply the formula. Students will determine the volume of figures composed of two right rectangular-prism solids.  While students will decompose simple 3 D shapes into two rectangular prisms, this decomposition is not required in the standard.  It is used here to help deepened student understanding.

Building Rectangular Prisms Part 2

This is the second part of a two-part volume lesson. In the first Building Rectangular Prisms (attached) lesson, foundational volume concepts are taught and students count cubes to find volume. In this lesson, students will discover the volume formulas length x width x height and base x height as they build rectangular prisms. They will use the formulas to find volume in real world situations.

Pump Up the Volume

In this 5E lesson, the students will explore the concept of volume. The students will build rectangular prisms, identify the dimensions of the prism and discover the volume of the prism.

Finding Volume (Utah Education Network)

In this lesson students will learn how to calculate and compare volumes of rectangular prisms.

Formulating Volume

Students will use situational stories to help them apply the formulas V = l × w × h and V = B × h  to find the volumes of right rectangular prisms with whole-number edge lengths.

Original Student Tutorial

Name Description
Video Game Store: Volume!

Help solve the problem of shipping video games and accessories to customers by calculating the volume of the containers needed in this interactive tutorial.

Problem-Solving Tasks

Name Description
Computing Volume Progression 1

Students are asked to determine the number of unit cubes needed to construct cubes with given dimensions.

Box of Clay

This purpose of this task is to help students understand what happens when you scale the dimensions of a right rectangular solid. This task provides an opportunity to compare the relative volumes of boxes in order to calculate the mass of clay required to fill them. These relative volumes can be calculated geometrically, filling the larger box with smaller boxes, or arithmetically using the given dimensions.

Surface Area and Volume

In this activity, students adjust the dimensions of either a rectangular or triangular prism and the surface area and volume are calculated for those dimensions. Students can also switch into compute mode where they are given a prism with certain dimensions and they must compute the surface area and volume. The application keeps score so students can track their progress. This application allows students to explore the surface area and volume of rectangular and triangular prisms and how changing dimensions affect these measurements. This activity also includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.

Teaching Idea

Name Description
Volume of Rectangular Prisms

This lesson is designed to introduce students to the concept of volume and how to find the volume of rectangular prisms. This lesson provides links to discussions and activities related to volume as well as suggested ways to integrate them into the lesson. Finally, the lesson provides links to follow-up lessons designed for use in succession with the current one.

Tutorial

Name Description
Volume: Decomposing a Solid Figure Example

This Khan Academy tutorial video illustrates finding the volume of an irregular figure made up of unit cubes by separating the figure into two rectangular prisms and finding the volume of each part.

Student Resources

Original Student Tutorial

Name Description
Video Game Store: Volume!:

Help solve the problem of shipping video games and accessories to customers by calculating the volume of the containers needed in this interactive tutorial.

Problem-Solving Tasks

Name Description
Computing Volume Progression 1:

Students are asked to determine the number of unit cubes needed to construct cubes with given dimensions.

Box of Clay:

This purpose of this task is to help students understand what happens when you scale the dimensions of a right rectangular solid. This task provides an opportunity to compare the relative volumes of boxes in order to calculate the mass of clay required to fill them. These relative volumes can be calculated geometrically, filling the larger box with smaller boxes, or arithmetically using the given dimensions.

Tutorial

Name Description
Volume: Decomposing a Solid Figure Example:

This Khan Academy tutorial video illustrates finding the volume of an irregular figure made up of unit cubes by separating the figure into two rectangular prisms and finding the volume of each part.



Parent Resources

Problem-Solving Tasks

Name Description
Computing Volume Progression 1:

Students are asked to determine the number of unit cubes needed to construct cubes with given dimensions.

Box of Clay:

This purpose of this task is to help students understand what happens when you scale the dimensions of a right rectangular solid. This task provides an opportunity to compare the relative volumes of boxes in order to calculate the mass of clay required to fill them. These relative volumes can be calculated geometrically, filling the larger box with smaller boxes, or arithmetically using the given dimensions.



Printed On:4/24/2024 3:51:48 PM
Print Page | Close this window