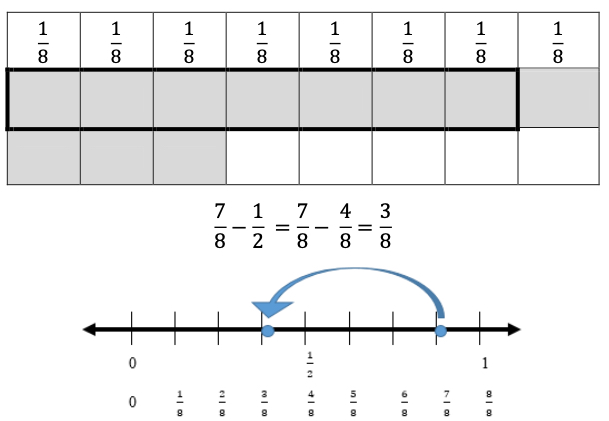
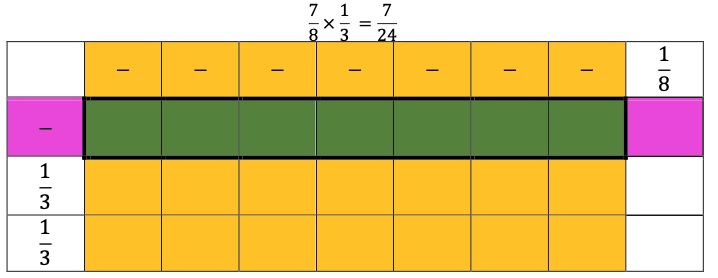
Solve real-world problems involving the addition, subtraction or multiplication of fractions, including mixed numbers and fractions greater than 1.
Shanice had a sleepover and her mom is making French toast in the morning. If her mom had
Instruction includes the use of visual models and equations to represent the problem.
| Name |
Description |
| Maris Has a Party | Students are given a word problem involving fractions with unlike denominators and are asked to estimate the sum, explain their reasoning, and then determine the sum. |
| Sarah’s Hike | Students are asked to estimate the difference between two fractional lengths and then calculate the difference. |
| Pizza Party | Students are asked to solve a word problem by finding the product of two fractions. |
| Just Run | Students are given a word problem involving subtraction of fractions with unlike denominators. Students are asked to determine if a given answer is reasonable, explain their reasoning, and calculate the answer. |
| Half of a Recipe | Students are asked to solve a word problem by finding the product of a fraction and a mixed number. |
| Candy at the Party | Students are asked to solve a word problem by finding the product of two mixed numbers. |
| Box Factory | Students are asked to solve a word problem by finding the product of two fractions. |
| Baking Cakes | Students are asked to estimate the sum of two mixed numbers and then calculate the sum. |
| Name |
Description |
| Disaster Relief | Students will analyze data to develop a resupply schedule for a humanitarian mission following a natural disaster. They will apply mathematical operations over multiple steps to minimize the operational cost of the humanitarian mission.
This is an open-ended engineering design lesson where students will develop a model to help them solve a problem. There are no “right” answers as the lesson is focused on the process of developing a solution and the skills and reasoning behind the process. Students should be given the freedom to interpret the problem and parameters in unique ways to pursue their own lines of thinking in producing a solution. |
| Voter Task Force | Students will help the Supervisor of Elections determine which voter registration locations could be improved to help more citizens get registered to vote. Students will learn about the number of citizens who registered to vote in a general election year compared to the total population of those eligible to vote. They will discuss which voter registration locations will provide the most access to citizens and allocate funds to help address the issue in this modeling eliciting activity.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.
|
| Let's Have a Fraction Party! | In this lesson, students will use addition and subtraction of fractions with unlike denominators to solve word problems involving situations that arise with the children who were invited to a party. They will use fraction strips as number models and connect the algorithm with these real-life word problems. |
| Fractions make the real WORLD problems go round | In this lesson students will use a graphic organizer to to solve addition and subtraction word problems. Students will create their own word problems in PowerPoint, by using pen and paper, or dry erase boards to help them to connect to and understand the structure of word problems. |
| Gimme Two Steps! | In this lesson, students will create representations for different multi-step word problems. One of these representations will be an expression with a variable. |
| Aaron and Anya's Discovery: Adding Fractions with Unlike Denominators | In this situational story, Aaron and Anya find several pieces of ribbon/cord of varying fractional lengths. They decide to choose 3 pieces and make a belt. All of the fractions have different denominators; students have to determine common denominators in order to add the fractional pieces. After students successfully add three fractional pieces, they make a belt and label it with their fractional pieces. |
| Real-World Fractions | This lesson focuses on providing students with real-world experiences where they will be required to multiply fractions. Students will be required to use visual fraction models or equations to represent the problem. This is a practice and application lesson, not an introductory lesson. |
| Babysitter's Club Fun with Fractions MEA | In this Model Eliciting Activity, MEA, students will apply their knowledge of adding, subtracting, and comparing fractions with like and unlike denominators. Babysitters 'R Us will require students to analyze data in the form of fractional units of time to select the best babysitter for the Cryin' Ryan family.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx |
| Multiplying a Fraction by a Fraction | In this lesson, students will solve problems related to training for a marathon to apply and make sense of multiplying fractions. The student will complete a function table to help illustrate patterns in the numerator/denominator relationships. This lesson utilizes the linear model as a concrete representation and moves towards the standard algorithm (a/b) x (c/d) = ac/bd. |
| Are You Ready for a Hurricane? | This activity allows students to determine the types of items that should be in a hurricane survival kit, use a budget and calculations to determine the items to include in the kit and gain an understanding of hurricanes and the need to prepare for them. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| More Bang for your Buck! | In this Model Eliciting Activity, MEA, students will work in teams to determine a procedure for ranking recycling companies. Students will need to calculate their return on recycling, make decisions based on a table of data, and write a letter to the client providing evidence for their decisions.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx |
| Estimating Fractions Using Benchmark Fractions 0, 1/2, or 1 | In this lesson, students use models (fractions tiles or number lines) to round fractions using benchmark fractions of 0, 1/2, or 1. |
| Garden Variety Fractions | Students explore the multiplication of a fraction times a fraction through story problems about a garden using models on Geoboards and pictorial representations on grid paper. Students make a connection between their models and the numerical representation of the equation. |
| Discovering Common Denominators | Students use pattern blocks to represent fractions with unlike denominators. Students discover that they need to convert the pattern blocks to the same size in order to add them. Therefore, they find and use common denominators for the addition of fractions. |
| Name |
Description |
| Computing Volume Progression 2 | Students are asked to find the volume of water in a tank that is 3/4 of the way full. |
| Computing Volume Progression 3 | Students are asked to find the height of a rectangular prism when given the length, width and volume. |
| Painting a Wall | The purpose of this task is for students to find the answer to a question in context that can be represented by fraction multiplication. This task is appropriate for either instruction or assessment depending on how it is used and where students are in their understanding of fraction multiplication. |
| Making Cookies | This tasks lends itself very well to multiple solution methods. Students may learn a lot by comparing different methods. Students who are already comfortable with fraction multiplication can go straight to the numeric solutions given below. Students who are still unsure of the meanings of these operations can draw pictures or diagrams. |
| Jog-A-Thon | The purpose of this task is to present students with a situation where it is natural to add fractions with unlike denominators; it can be used for either assessment or instructional purposes. Teachers should anticipate two types of solutions: one where students calculate the distance Alex ran to determine an answer, and one where students compare the two parts of his run to benchmark fractions. |
| To Multiply or not to multiply? | The purpose of this task is to familiarize students with multiplying fractions with real-world questions. |
| Salad Dressing | The purpose of this task is to have students add fractions with unlike denominators and divide a unit fraction by a whole number. This accessible real-life context provides students with an opportunity to apply their understanding of addition as joining two separate quantities. |
| Running to School | The task could be one of the first activities for introducing the multiplication of fractions. The task has fractions which are easy to draw and provides a linear situation. Students benefit from reasoning through the solution to such word problems before they are told that they can be solved by multiplying the fractions; this helps them develop meaning for fraction multiplication. |
| Half of a Recipe | This is the third problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. The first, Running to school, does not require that the unit fractions that comprise 3/4 be subdivided in order to find 1/3 of 3/4. The second task, Drinking Juice, does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. This task also requires subdivision and involves multiplying a fraction and a mixed number. |
| Drinking Juice | This is the second problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. This task does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. |
| Do These Add Up? | This task addresses common errors that students make when interpreting adding fractions word problems. It is very important for students to recognize that they only add fractions when the fractions refer to the same whole, and also when the fractions of the whole being added do not overlap. This set of questions is designed to enhance a student's understanding of when it is and is not appropriate to add fractions. |
| Name |
Description |
| Computing Volume Progression 2: | Students are asked to find the volume of water in a tank that is 3/4 of the way full. |
| Computing Volume Progression 3: | Students are asked to find the height of a rectangular prism when given the length, width and volume. |
| Painting a Wall: | The purpose of this task is for students to find the answer to a question in context that can be represented by fraction multiplication. This task is appropriate for either instruction or assessment depending on how it is used and where students are in their understanding of fraction multiplication. |
| Making Cookies: | This tasks lends itself very well to multiple solution methods. Students may learn a lot by comparing different methods. Students who are already comfortable with fraction multiplication can go straight to the numeric solutions given below. Students who are still unsure of the meanings of these operations can draw pictures or diagrams. |
| Jog-A-Thon: | The purpose of this task is to present students with a situation where it is natural to add fractions with unlike denominators; it can be used for either assessment or instructional purposes. Teachers should anticipate two types of solutions: one where students calculate the distance Alex ran to determine an answer, and one where students compare the two parts of his run to benchmark fractions. |
| To Multiply or not to multiply?: | The purpose of this task is to familiarize students with multiplying fractions with real-world questions. |
| Salad Dressing: | The purpose of this task is to have students add fractions with unlike denominators and divide a unit fraction by a whole number. This accessible real-life context provides students with an opportunity to apply their understanding of addition as joining two separate quantities. |
| Running to School: | The task could be one of the first activities for introducing the multiplication of fractions. The task has fractions which are easy to draw and provides a linear situation. Students benefit from reasoning through the solution to such word problems before they are told that they can be solved by multiplying the fractions; this helps them develop meaning for fraction multiplication. |
| Half of a Recipe: | This is the third problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. The first, Running to school, does not require that the unit fractions that comprise 3/4 be subdivided in order to find 1/3 of 3/4. The second task, Drinking Juice, does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. This task also requires subdivision and involves multiplying a fraction and a mixed number. |
| Drinking Juice: | This is the second problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. This task does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. |
| Do These Add Up?: | This task addresses common errors that students make when interpreting adding fractions word problems. It is very important for students to recognize that they only add fractions when the fractions refer to the same whole, and also when the fractions of the whole being added do not overlap. This set of questions is designed to enhance a student's understanding of when it is and is not appropriate to add fractions. |
| Name |
Description |
| Computing Volume Progression 2: | Students are asked to find the volume of water in a tank that is 3/4 of the way full. |
| Computing Volume Progression 3: | Students are asked to find the height of a rectangular prism when given the length, width and volume. |
| Painting a Wall: | The purpose of this task is for students to find the answer to a question in context that can be represented by fraction multiplication. This task is appropriate for either instruction or assessment depending on how it is used and where students are in their understanding of fraction multiplication. |
| Making Cookies: | This tasks lends itself very well to multiple solution methods. Students may learn a lot by comparing different methods. Students who are already comfortable with fraction multiplication can go straight to the numeric solutions given below. Students who are still unsure of the meanings of these operations can draw pictures or diagrams. |
| Jog-A-Thon: | The purpose of this task is to present students with a situation where it is natural to add fractions with unlike denominators; it can be used for either assessment or instructional purposes. Teachers should anticipate two types of solutions: one where students calculate the distance Alex ran to determine an answer, and one where students compare the two parts of his run to benchmark fractions. |
| To Multiply or not to multiply?: | The purpose of this task is to familiarize students with multiplying fractions with real-world questions. |
| Salad Dressing: | The purpose of this task is to have students add fractions with unlike denominators and divide a unit fraction by a whole number. This accessible real-life context provides students with an opportunity to apply their understanding of addition as joining two separate quantities. |
| Running to School: | The task could be one of the first activities for introducing the multiplication of fractions. The task has fractions which are easy to draw and provides a linear situation. Students benefit from reasoning through the solution to such word problems before they are told that they can be solved by multiplying the fractions; this helps them develop meaning for fraction multiplication. |
| Half of a Recipe: | This is the third problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. The first, Running to school, does not require that the unit fractions that comprise 3/4 be subdivided in order to find 1/3 of 3/4. The second task, Drinking Juice, does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. This task also requires subdivision and involves multiplying a fraction and a mixed number. |
| Drinking Juice: | This is the second problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. This task does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. |
| Do These Add Up?: | This task addresses common errors that students make when interpreting adding fractions word problems. It is very important for students to recognize that they only add fractions when the fractions refer to the same whole, and also when the fractions of the whole being added do not overlap. This set of questions is designed to enhance a student's understanding of when it is and is not appropriate to add fractions. |
-1.png)

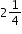
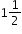 loaves for the French toast, how much bread does she have left?
loaves for the French toast, how much bread does she have left?