Standard #: MA.5.FR.2.2

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.5.NSO.2.1
• MA.5.NSO.2.4
• MA.5.AR.1.2
• MA.5.GR.2.1

 

Terms from the K-12 Glossary

• NA

 

Vertical Alignment

Previous Benchmarks

• MA.4.FR.2.4

 

Next Benchmarks

• MA.6.NSO.2.2

 

Purpose and Instructional Strategies

The purpose of this benchmark is for students to learn strategies to multiply two fractions. This continues the work from grade 4 where students multiplied a whole number times a fraction and a fraction times a whole number (MA.4.FR.2.4). Procedural fluency will be achieved in grade 6 (MA.6.NSO.2.2). 

• During instruction, students are expected to multiply fractions including proper fractions, improper fractions (fractions greater than 1), and mixed numbers efficiently and accurately. 
• Visual fraction models (area models, tape diagrams, number lines) should be used and created by students during their work with this benchmark (MTR.2.1). Visual fraction models should show how a fraction is partitioned into parts that are the same as the product of the denominators. 

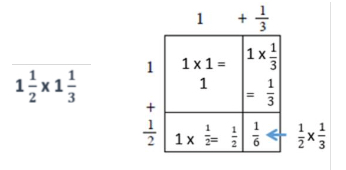
• When exploring an algorithm to multiply fractions ($\frac{\text{a}}{\text{b}}$ × $\frac{\text{c}}{\text{d}}$= $\frac{\text{a x c}}{\text{b x d}}$ ), make connections to an accompanying area model. This will help students understand the algorithm conceptually and use it more accurately. 
• Instruction includes students using equivalent fractions to simplify answers; however, putting answers in simplest form is not a priority.

 

Common Misconceptions or Errors

• Students may believe that multiplication always results in a larger number. Using models when multiplying with fractions will enable students to generalize about multiplication algorithms that are based on conceptual understanding (MTR.5.1). 
• Students can have difficulty with word problems when determining which operation to use, and the stress of working with fractions makes this happen more often. 
  • For example, “Mark has $\frac{\text{3}}{\text{4}}$ yards of rope and he gives a third of the rope to a friend. How much rope does Mark have left?” expects students to first find $\frac{\text{1}}{\text{3}}$ of $\frac{\text{3}}{\text{4}}$, or multiply $\frac{\text{1}}{\text{3}}$ x $\frac{\text{3}}{\text{4}}$, and then to find the difference to find how much Mark has left. On the other hand, "Mark has $\frac{\text{3}}{\text{4}}$ yards of rope to a friend. How much rope does Mark have left?” only requires finding the difference $\frac{\text{3}}{\text{4}}$ - $\frac{\text{1}}{\text{3}}$.

 

Strategies to Support Tiered Instruction

• Instruction involves real-world examples and models which allow students to see that multiplication does not always result in a larger number. 
  • For example, the teacher provides the problem: “Tau has $\frac{\text{1}}{\text{4}}$ of the lasagna pan leftover from the party in the refrigerator. He eats one half of the leftovers for dinner. How much of the lasagna did he eat for dinner?” This can be written as $\frac{\text{1}}{\text{2}}$ x $\frac{\text{1}}{\text{4}}$ or $\frac{\text{1}}{\text{2}}$ "of" $\frac{\text{1}}{\text{4}}$

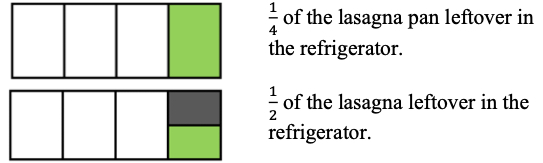
• When students think about what is left in the refrigerator now, they must think in terms of the whole pan of lasagna. Tau didn’t eat half the pan; he ate half of the portion that was left. So how much of the whole pan did he eat?

 

Instructional Tasks

Instructional Task 1 (MTR.4.1, MTR.7.1) 

• Part A. Martiza has 4$\frac{\text{1}}{\text{2}}$ cups of cream cheese. She uses $\frac{\text{3}}{\text{4}}$ of the cream cheese for a banana pudding recipe. After she uses it for the recipe, how much cream cheese will Maritza have left? 
• Part B. To find out how much cream cheese she used, Maritza multiplied 4 $\frac{\text{1}}{\text{2}}$ × $\frac{\text{3}}{\text{4}}$ as (4 × $\frac{\text{3}}{\text{4}}$) + ($\frac{\text{1}}{\text{2}}$ × $\frac{\text{3}}{\text{4}}$). Will this method work? Why or why not? 
• Part C. What additional step is required to find how much cream cheese she has left?

 

Instructional Items

Instructional Item 1

What is the product of $\frac{\text{1}}{\text{5}}$ x 6 $\frac{\text{1}}{\text{2}}$?

• a. $\frac{\text{6}}{\text{10}}$
• b. $\frac{\text{12}}{\text{5}}$
• c. 6 $\frac{\text{7}}{\text{10}}$
• d. 1 $\frac{\text{3}}{\text{10}}$ 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.