General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- NA
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to understand that when adding or subtracting fractions with unlike denominators, equivalent fractions are generated to rewrite the fractions with like denominators, with which students have experience from grade 4 (MA.4.FR.2.2). Procedural fluency will be achieved in grade 6 (MA.6.NSO.2.3).- During instruction, have students begin with expressions with two fractions that require the rewriting of one of the fractions (where one denominator is a multiple of the other, like 1 + 3 or + ) and progress to expressions where both fractions must be rewritten (where denominators are not multiples of one another, like + or 1 + 9 ). In doing so, students can explore how both fractions need like denominators to make addition and subtraction easier. Once students have stronger conceptual understanding, expressions requiring adding or subtracting 3 or more numbers should be included in instruction.
- It is important for students to practice problems that include various fraction models as students may find that a circular model might not be the best model when adding or subtracting fractions because of the difficulty in partitioning the pieces so they are equal (MTR.2.1).
- When students use an algorithm to add or subtract fractions, encourage students’ use of
flexible strategies.
- For example, students can use a partial sums strategy when adding 1 + 4 by adding the whole numbers 1 + 4 together first before adding the fractional parts and regrouping when necessary.
- Mental computations and estimation strategies should be used to determine the
reasonableness of solutions.
- For example, when adding 1 + 4 , students could reason that the sum will be greater than 6 because the sum of the whole numbers is 5 and the sum of the fractional parts in the mixed numbers will be greater than 1. Keep in mind that estimation is about getting reasonable solutions and not about getting exact solutions, therefore allow for flexible estimation strategies and expect students to justify them.
- Although not required, instruction may include students using equivalent fractions to simplify answers.
Common Misconceptions or Errors
- Students can carry misconceptions from grade 4 about adding and subtracting fractions and understanding why the denominator remains the same. Emphasize the use of area and number line models, and present expressions in numeral-word form to help understand that the denominator is the unit.
- For example, “5 eighths + 9 eighths is equal to how many eighths?”
- Students often try to use different models when adding, subtracting or comparing
fractions.
- For example, they may use a circle for thirds and a rectangle for fourths, when comparing fractions with thirds and fourths.
- Remind students that the representations need to be from the same whole models with the
same shape and same size. In a real-world problem, this often looks like same units.
- For example, “Trey has 1 cups of water and Rachel has 2 cups of water. How many cups of water do they have?”
Strategies to Support Tiered Instruction
- Instruction includes concrete models and drawings that help solidify understanding that when adding and subtracting with unlike denominators, the value of the fractional parts remains the same.
- For example, students create a model for each of the fractions in the problem − .

- It is important for students to draw these two models the same size. Once the models are created, students will then need to be able to make all the pieces within each model the same size to be able to subtract. They then divide each piece of the model into fourths. They then divide each piece of the model into thirds. Now both models are divided in to 12 pieces and the subtraction problem can be represented as − . It is important to note that the area of the models did not change. Just because the fraction changed, the value of the fraction did not change.
- Instruction includes concrete models and drawings that help solidify understanding that when adding and subtracting with unlike denominators, students are adding and subtracting pieces of the whole.
- For example, the teacher emphasizes the use of area and number line models and presents expressions in numeral-word form to help understand that one over the denominator is the unit.
- For example, “3 twelfths + 6 twelfths are equal to how many twelfths?” The denominator is 12 so one unit is equal to 1 twelfth.
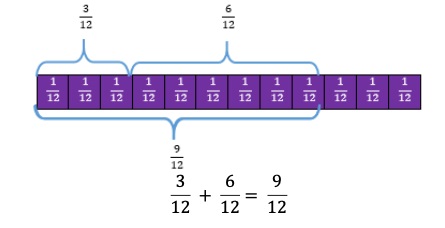
Instructional Tasks
Instructional Task 1 (MTR.2.1)
Write an expression for the visual model below. Then find the sum.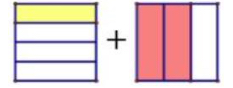
Instructional Task 2 (MTR.2.1)
Use a visual fraction model to find the value of the expression + .
Instructional Task 3 (MTR.3.1)
Find the value of the expression 3 + .
Instructional Task 4 (MTR.3.1)
Find the differences − and 2 − .
Instructional Items
Instructional Item 1
Find the sum + .- a. 1
- b.
- c. 1
- d.
Instructional Item 2
- a. 1
- b. 1
- c. 1
- d. 2
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive

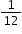 and
and 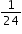 can be determined as
can be determined as 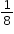 ,
,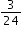 ,
, 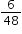 or
or 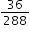 by using different common denominators or equivalent fractions.
by using different common denominators or equivalent fractions.