General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- NA
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to understand that a division expression can be written as a fraction by explaining their thinking when working with fractions in various contexts. This builds on the understanding developed in grade 4 that remainders are fractions (MA.4.NSO.2.4), and prepares students for the division of fractions in grade 6 (MA.6.NSO.2.2).- When students read as "five-eights," they should be taught that can also be interpreted as “5 divided by 8,” where 5 represents the numerator and 8 represents the denominator of the fraction (5 = 5 ÷ 8) and refers to 5 wholes divided into 8 equal parts.
- Teachers can activate students' prior knowledge of fractions as division by using fractions that represent whole numbers (e.g., ). Familiar division expressions help build students’ understanding of the relationship between fractions and division (MTR.5.1).
- During instruction, provide examples accompanied by area and number line models.
- When solving mathematical or real-world problems involving division of whole numbers and interpreting the quotient in the context of the problem, students will be able to represent the division of two whole numbers as a mixed number, where the remainder is the fractional part’s numerator and the size of a group is its denominator (for example, 17 ÷ 3 equals 5 which is the number of size 3 groups you can make from 17 objects 3 including the fractional group). Students should demonstrate their understanding by explaining or illustrating solutions using visual fraction models or equations.
Common Misconceptions or Errors
- Students can believe that the fraction bar represents subtraction in lieu of understanding that the fraction bar represents division.
- Students can have the misconception that division always results in a smaller number.
- Students can presume that dividends must always be greater than divisors and, thus, reorder when representing a division expression as a fraction. Show students examples of fractions with greater numerators and greater denominators to create a division equation.
Strategies to Support Tiered Instruction
- Instruction includes making the connection to models and tools previously used to understand division as equal groups or sharing, but now as a fraction in a real-world
context.
- For example, “Eight friends share four brownies” can be represented as . This 8 means that 4 ÷ 8 can be represented using the model below. Four is divided into 8 equal parts, each part is of the brownie.

- Connecting the real-world application to the fraction will help students understand that the fraction really means division.
- Instruction includes making the connection to models and tools previously used to understand division as equal groups or sharing, but now as a fraction in a real-world context.
- For example, “Marcos has 8 toy cars that he wants to put into 4 boxes equally. How many cars can go in each box?” 8 ÷ 4 can be shown using a model of 8 wholes divided into 4 groups. The quotient would be the total number of pieces in each group. The model below would show that 8 ÷ 4 = 2. This can also be expressed as = 2.
- Instruction includes examples of fractions with greater numerators and greater denominators to create a division equation.
Instructional Tasks
Instructional Task 1 (MTR.7.1)
Create a real-world division problem that results in an answer equivalent to .
Instructional Task 2 (MTR.3.1)
Write a mixed number that is equivalent to 10 ÷ 3.
Instructional Task 3 (MTR.7.1)
Monica has a ribbon that is 8 feet long. She wants to make 12 bows for her friends. How long will each piece of the ribbon be? Express your answer in both feet and inches.
Instructional Task 4 (MTR.7.1)
Albert baked 18 fudge brownies for his video game club members. He wants to share the brownies with the 5 club members. How many brownies will each club member get?
Instructional Items
Instructional Item 1
Which expression is equivalent to ?- a. 7−12
- b. 7÷12
- c. 12−7
- d. 12÷7
Instructional Item 2
Amanda has 12 pepperoni slices that need to be distributed equally among 5 mini pizzas. How many pepperoni slices will go on each mini pizza?- a.
- b. 2
- c. 7
- d. 60
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.

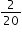 of a gallon of lemonade which is equivalent to one-tenth of a gallon which is a little more than 12 ounces.
of a gallon of lemonade which is equivalent to one-tenth of a gallon which is a little more than 12 ounces.