Standard #: MA.5.NSO.2.3


This document was generated on CPALMS - www.cpalms.org



Add and subtract multi-digit numbers with decimals to the thousandths, including using a standard algorithm with procedural fluency.


General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 5
Strand: Number Sense and Operations
Standard: Add, subtract, multiply and divide multi-digit numbers.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Equation
  • Expression

 

Vertical Alignment

Previous Benchmarks

 

Next Benchmarks

 

Purpose and Instructional Strategies

The purpose of this benchmark is for students to add and subtract multi-digit numbers with decimals to the thousandths with procedural fluency. In grade 4 (MA.4.NSO.2.7), students explored the addition and subtraction of multi-digit numbers with decimals to hundredths using money and manipulatives. In grade 6, students add and subtract positive fractions with procedural fluency. 
  • To demonstrate procedural fluency, students may choose a standard algorithm that works best for them and demonstrates their procedural fluency. A standard algorithm is a method that is efficient and accurate (MTR.3.1). 
  • When students use a standard algorithm, they should be able to justify why it works conceptually. Teachers can expect students to demonstrate how their algorithm works, for example, by comparing it to another method for addition and subtraction (MTR.6.1). 
  • Along with using a standard algorithm, students should estimate reasonable solutions before solving. Estimation helps students anticipate possible answers and evaluate whether their solutions make sense after solving.

 

Common Misconceptions or Errors

  • Students can make computational errors while using standard algorithms when they cannot reason why their algorithms work. In addition, they can struggle to determine where or why that computational mistake occurred because they did not estimate reasonable values for intermediate outcomes as well as for the final outcome. During instruction, teachers should expect students to justify their work while using their chosen algorithms and engage in error analysis activities to connect their understanding to the algorithm.

 

Strategies to Support Tiered Instruction

  • Instruction includes estimating reasonable values for sums and differences when adding and subtracting decimals to the hundredths. 
    • For example, students make reasonable estimates for the sum of 6.32 + 2.84. Instruction includes stating, “Before using an algorithm, we will estimate the sum to make sure that we are using the algorithm correctly and our answer is reasonable. I will use my understanding of rounding decimals to estimate my sum. The addend of 6.32 rounds to 6 when rounded to the nearest whole number and reasonable estimate for my sum would be 9 because 6 + 3 = 9.” 
    • For example, students make reasonable estimates for the difference of 7.9 − 4.25. Instruction includes stating, “Before using an algorithm, we will estimate the difference to make sure that we are using the algorithm correctly and our answer is reasonable. I will use my understanding of rounding decimals to estimate my difference. The minuend of 7.9 rounds to 8 when rounded to the nearest whole number and the subtrahend 4.25 rounds to 4 when rounded to the nearest whole number. A reasonable estimate for my difference would be 4 because 8 − 4 = 4.” the addend 2.84 rounds to 3 when rounded to the nearest whole number. 
  • Instruction includes explaining and justifying mathematical reasoning while using an algorithm to add and subtract decimals to the hundredths. Instruction also includes determining if an algorithm was used correctly by analyzing any errors made and reviewing the reasonableness of solutions.
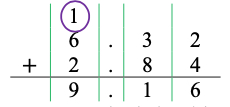
  • For example, students use a standard algorithm to determine 6.32 + 2.84 and explain their thinking using a place value understanding. Instruction includes stating, “Begin by lining up the decimal points and place values for each addend. Next, add in hundredths place. 2 hundredths plus 4 hundredths are 6 hundredths. Because the total number of hundredths is less than 10 hundredths it is not necessary to regroup. Next, add in the tenths place. 3 tenths plus 8 tenths are 11 tenths. Because I have more than 10 tenths it is necessary to regroup the 10 tenths to make one whole. After composing a group of 10 tenths there is 1 tenth remaining. Finally, add 6 ones plus 2 ones and the 1 whole that was regrouped from the tenths place. The sum is 9.16. Our sum of 9.16 is close to our estimate of 9, this helps us determine that our answer is reasonable.”
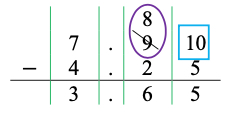
standard algorithm
  • For example, students use a standard algorithm to determine 7.9 − 4.25 and explain their thinking using place value understanding. The teacher reminds students that 7.9 is equivalent to 7.90 and uses a decimal grid to show the equivalency of 0.9 and 0.90 if needed. Instruction includes stating, “Begin by lining up the decimal points and place values. Next, subtract 4.25 starting in the hundredths place. There are not enough hundredths to subtract 5 hundredths from 0 hundredths. It is necessary to decompose one tenth into 10 hundredths. Now there are 10 hundredths, and there is enough to subtract 5 hundredths. 10 hundredths − 5 hundredths = 5 hundredths. Then, subtract the tenths: 8 tenths − 2 tenths = 6 tenths. Finally, subtract the ones: 7 ones − 4 ones = 3 ones. The difference is 3.65. Our difference of 3.65 is close to our estimate of 4, this helps us determine that our answer is reasonable.” 
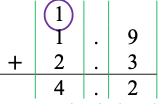
standard algorithm
  • For example, students use a standard algorithm to determine 1.9 + 2.3 and explain their thinking using a place value understanding. Instruction includes stating, “Begin by lining up the decimal points and place values for each addend. Next, add in tenths place. 9 tenths plus 3 tenths are 12 tenths. Because I have more than 10 tenths it is necessary to regroup the 10 tenths to make one whole. After composing a group of 10 tenths there are 2 tenths remaining. Finally, add 1 one plus 2 ones and the 1 whole that was regrouped from the tenths place. The sum is 4.2. Our sum of 4.2 is close to our estimate of 4, this helps us determine that our answer is reasonable.” 
standard algorithm
  • For example, students use a standard algorithm to determine 5.2 − 3.8 and explain their thinking using place value disks and their understanding of place value. Instruction includes stating, “Begin by lining up the decimal points and place values. Next, subtract 3.8 starting in the tenths place. There are not enough tenths to subtract 8 tenths from 2 tenths. It is necessary to decompose one whole into 10 tenths. Now there are a total of 12 tenths, and there are enough to subtract 8 tenths. 12 tenths – 8 tenths = 4 tenths. Finally, subtract the ones: 4 ones – 3 ones = 1 one. The difference is 1.4. Our difference of 1.4 is close to our estimate of 1, this helps us determine that our answer is reasonable.” 
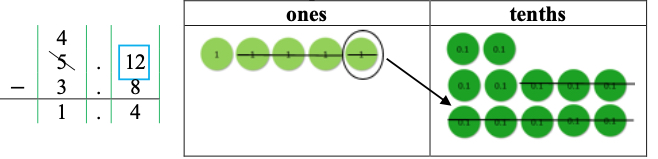
standard algorithm
  • Instruction includes the use of place value columns to support place value understanding when using an algorithm to add and subtract decimals.

 

Instructional Tasks

Instructional Task 1 (MTR.3.1) 

Use a standard algorithm to find the difference of eight hundred two and forty - Six thousandths and three hundred and nine tenths. Explain how you use your algorithm to subtract.

 

Instructional Items

Instructional Item 1

Find the sum and difference of 8.72 and 3.032. 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.



Related Courses

Course Number1111 Course Title222
5012070: Grade Five Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7712060: Access Mathematics Grade 5 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012065: Grade 4 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))
5012015: Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.5.NSO.2.AP.3 Apply a strategy to add and subtract multi-digit numbers with decimals to the tenths (e.g., 3.3 + 0.5) and hundredths (e.g., 1.25 − 0.12). Multi-digit numbers not to exceed 9.99.


Related Resources

Educational Games

Name Description
Ice Ice Maybe: An Operations Estimation Game


This fun and interactive game helps practice estimation skills, using various operations of choice, including addition, subtraction, multiplication, division, using decimals, fractions, and percents.

Various levels of difficulty make this game appropriate for multiple age and ability levels.

Addition/Subtraction: The addition and subtraction of whole numbers, the addition and subtraction of decimals.

Multiplication/Division: The multiplication and addition of whole numbers.

Percentages: Identify the percentage of a whole number.

Fractions: Multiply and divide a whole number by a fraction, as well as apply properties of operations.

Change Maker

This interactive applet gives students practice in making change in U.S. dollars and in four other currencies. Students are presented with a purchase amount and the amount paid, and they must enter the quantity of each denomination that make up the correct change. Students are rewarded for correct answers and are shown the correct change if they err. There are four levels of difficulty, ranging from amounts less than a dollar to amounts over $100.

Formative Assessments

Name Description
Running A Race

Students are asked to solve a word problem that involves adding two decimals by using a strategy based on place value.

Tony’s Lunchbox

Students are asked to solve a word problem that involves subtracting two decimals by using a strategy based on place value.

Lesson Plans

Name Description
Catch Me If You Can: Engineering Design Challenge

In this lesson, 5th grade students work in small groups on a STEM challenge that involves science and math standards related to the water cycle, as well as learning the engineering design process.

Weathering Weather

This is a design challenge lesson allowing students to utilize their understanding of climate zones to design a tropical roof that would withstand the wind and water generated by a hurricane. This lesson also allows you to assess students understanding of operations with decimals to create their design under a given budget.

Icky, Icky, No More Slicky

In this lesson, 5th grade students will build an engineering device to separate oil from water in a simulated oil spill. Students will have an opportunity to learn about the impact that humans can have on the environment, both positively and negatively.

This is an Engineering Design Challenge that is best used after a unit or lesson that is aligned to science standards on solving problems or materials which dissolve in water. This challenge provides students a means to use their knowledge of the way materials will or will not dissolve in water to create and design an oil spill removal tool while learning the Engineering Design Process and being exposed to the field of engineering. This lesson is not intended as an initial introduction to the standard and would be best utilized as a culmination lesson.

The Coasta with the Mosta

Students will create an exciting and thrilling roller coaster model. Students will use their knowledge of forces to build a model of a roller coaster using foam insulation and a marble.

When the Wind Blows

This is an engineering design process lesson that covers forces and motion. It is designed to engage students using hands-on problem solving strategies.

Bottling Rockets

In this lesson, students will explore the concepts of force and motion as they use the engineering design process to create and test rockets. Students will demonstrate their understanding of familiar forces by creating and presenting a poster. Take students up, up, and away with this engaging lesson!

From Trash to Treasure - An Engineering Design Challenge

This lesson gives students hands-on experience with sorting mixtures based on their properties. The students will relate these science standards to a real-world problem of eliminating trash in land fills. They will have to purchase the tools they use to create their assembly line to sort the garbage within the budget provided.

Bridge Over Troubled Waters

In this engineering lesson, students will design and construct a bridge that will be free-standing and support a toy car.

Medic Mass Landing: Engineering Design Challenge

In this lesson, 5th grade students work in small groups on a STEM challenge that involves science and math standards related to force, motion, and measurement, as well as learning the engineering design process.

Shopping for My Trip to the Beach

This lesson will provide practice in adding/subtracting decimals in money form.  Student will model with base-ten blocks and then using the standard algorithm, through the hundredths place. This is not an introductory lesson. Students should already have conceptual knowledge and practice adding four-digit numbers using manipulatives or other methods.

Where Will We Stay?

In this lesson, students explore lodging options for their dream family vacation. Students will plan a vacation for a family of four. With a budget of $5,000 students will prepare a budget to include the cost of transportation, lodging, and attractions. In this lesson, students will focus on preparing the budget for hotel costs. In lesson 1 of this unit lesson, students prepared a budget for transportation. In the subsequent lesson to this one, students will prepare a budget for the entertainment/attractions costs portion of their vacation. Teachers can choose to do one, some, or all lessons as they can be completed independently of one another.

Keeping Your Cool With Your Lunch Bag

On this MEA activity, students will create a procedure to rank five lunch bags as to which one is the best in keeping food and drinks at a safe temperature and appealing to the taste, while keeping design and price on target.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.

Kudos for Kicks - MEA

In this Model Eliciting Activity, MEA, the students will be asked to assist a discount shoe store owner, who is planning a one day sale promotion, to choose a famous brand shoe to feature for the one day sale. Students will determine which one will bring in more customers, as well as provide the most profit. Students will need to read a data table, calculate the total profit margin per pair, and the total sales potential profit margin determined by the number of sneakers in stock. Students will also need to consider comfort, durability, and specific details about each brand. A twist is added to the problem when additional stock items are added, plus one of the brands is removed and two new brands are added.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

To Oregon by Wagon

Students work in teams to plan the contents of a covered wagon for a family relocating from Missouri to Oregon. Students must calculate the weight and cost of the wagon by adding, subtracting, and multiplying with decimals.

Out to Lunch: Decimal Operations with a Menu

In this lesson students work toward fluency with decimal operations by using a snack bar menu and going "Out to Lunch" with a friend.

A Tasty Treat

In this lesson, students will be given a list of ingredients and prices they must use to create their own snack mix. Students will have to add, subtract, multiply, and divide decimal numbers. The closure of the lesson focuses specifically on the division strategies students used to solve the problem.

Party Planners Wanted

In this Model Eliciting Activity, MEA, students will work in collaborative groups to solve multistep problems with whole numbers and decimals by using different mathematical operations such as addition, subtraction, multiplication, and division. The students will be asked to assist a businessman who is planning a party for his employees. They will need to read several ads and decide which company offers the best deal in renting tables, chairs, and tablecloths for the client. They will need to take into consideration the number of guests attending the party and the budget allowed. A twist is added to the problem when the students are asked to consider an additional ad and the fact that the guest list is now slightly larger.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

Pick A Pet

This Model Eliciting Activity (MEA) asks students to develop a procedure for choosing a reptile or amphibian to place in a school reception area. Students will need to consider safety, price of animal, cost by week to feed animal, size and cost of the enclosure, and the life span of the animals they are considering. In the second portion of the problem statement, the students will need to prepare a budget and cost analysis for the year to consider if they have still made the correct choices while adding three more animals for consideration. The culminating activity for this MEA will have the student write a proposal for the Principal to state their choice of animal, give a year's budget for cost and care for the animal.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

The Mystery of Decimals

This lesson reviews all four operations (adding, subtracting, multiplying, and dividing) with decimals. It is designed to easily provide differentiated instruction for students. The culmination of the lesson is a computer-based assessment which provides a fun change from a typical pencil and paper test.

“Dinner with Friends”

The students will determine what to order at a dinner with friends yet stay within a budget. The students will try to maximize their budgets and order as much food as they possibly can with their given amount of money.

Race to Fill the Whole!

In this engaging lesson, students will play a game using base ten blocks to add decimals to the hundredths.

Original Student Tutorials

Name Description
Sailing Through Subtracting Decimals

Sail through subtracting decimals to the thousandths place using a standard algorithm in this interactive tutorial.

Add Another Topping: Adding Decimals

Learn to add decimals to the thousandths using a standard algorithm at the ice cream shop in this interactive tutorial. 

Perspectives Video: Experts

Name Description
Fluency vs. Automaticity

How are fluency and automaticity defined? Dr. Lawrence Gray explains fluency and automaticity in the B.E.S.T. mathematics benchmarks in this Expert Perspectives video.

The Role of Procedures in Fluency

What are the components to a good procedure? Dr. Lawrence Gray discusses the role of procedures in the path to fluency in this Expert Perspectives video.

That's Not How I Learned it: Why today's math may look different

Why do students need "a" good procedure for the arithmetic operations? Dr. Lawrence Gray explains why math may look different than in the past in this Expert Perspectives video.

B.E.S.T. Journey

What roles do exploration, procedural reliability, automaticity, and procedural fluency play in a student's journey through the B.E.S.T. benchmarks? Dr. Lawrence Gray explains the path through the B.E.S.T. mathematics benchmarks in this Expert Perspectives video.

What is Fluency?

What is fluency? What are the ingredients required to become procedurally fluent in mathematics? Dr. Lawrence Gray explores what it means for students to be fluent in mathematics in this Expert Perspectives video.

Why Isn't Getting the "Right" Answer Good Enough?

Why is it important to look beyond whether a student gets the right answer? Dr. Lawrence Gray explores the importance of understanding why we perform certain steps or what those steps mean, and the impact this understanding can have on our ability to solve more complex problems and address them in the context of real life in this Expert Perspectives video.

A Standard Algorithm

Ever wonder why the benchmarks say, “a standard algorithm,” instead of, “the standard algorithm?" Dr. Lawrence Gray explores the role that standard algorithms can play in building and exhibiting procedural fluency through this Expert Perspectives video.

Teaching Idea

Name Description
Guide for Providers: Best Practices For K–5 Mathematics Support During Out-Of-School Time

This guide offers five practical strategies to help after-school providers support meaningful, low-pressure math experiences that lead to deeper understanding and better long-term outcomes for K-5 students.

Tutorial

Name Description
Adding and Subtracting with Decimals

This tutorial for student audiences will assist learners with a further understanding of the rules for adding and subtracting with decimals. Students will be able to navigate the teaching portion of the tutorial at their own pace and test their understanding after each step of the lesson with a "Try This" section. The "Try This" section will monitor students answers and self-check by a right answer turning orange and a wrong answer dissolving.

Worksheet

Name Description
Open Number Line

Open Number Line

Student Resources

Original Student Tutorials

Name Description
Sailing Through Subtracting Decimals:

Sail through subtracting decimals to the thousandths place using a standard algorithm in this interactive tutorial.

Add Another Topping: Adding Decimals:

Learn to add decimals to the thousandths using a standard algorithm at the ice cream shop in this interactive tutorial. 

Educational Games

Name Description
Ice Ice Maybe: An Operations Estimation Game:


This fun and interactive game helps practice estimation skills, using various operations of choice, including addition, subtraction, multiplication, division, using decimals, fractions, and percents.

Various levels of difficulty make this game appropriate for multiple age and ability levels.

Addition/Subtraction: The addition and subtraction of whole numbers, the addition and subtraction of decimals.

Multiplication/Division: The multiplication and addition of whole numbers.

Percentages: Identify the percentage of a whole number.

Fractions: Multiply and divide a whole number by a fraction, as well as apply properties of operations.

Change Maker:

This interactive applet gives students practice in making change in U.S. dollars and in four other currencies. Students are presented with a purchase amount and the amount paid, and they must enter the quantity of each denomination that make up the correct change. Students are rewarded for correct answers and are shown the correct change if they err. There are four levels of difficulty, ranging from amounts less than a dollar to amounts over $100.

Tutorial

Name Description
Adding and Subtracting with Decimals:

This tutorial for student audiences will assist learners with a further understanding of the rules for adding and subtracting with decimals. Students will be able to navigate the teaching portion of the tutorial at their own pace and test their understanding after each step of the lesson with a "Try This" section. The "Try This" section will monitor students answers and self-check by a right answer turning orange and a wrong answer dissolving.

Worksheet

Name Description
Open Number Line:

Open Number Line



Parent Resources

Teaching Idea

Name Description
Guide for Providers: Best Practices For K–5 Mathematics Support During Out-Of-School Time:

This guide offers five practical strategies to help after-school providers support meaningful, low-pressure math experiences that lead to deeper understanding and better long-term outcomes for K-5 students.

Tutorial

Name Description
Adding and Subtracting with Decimals:

This tutorial for student audiences will assist learners with a further understanding of the rules for adding and subtracting with decimals. Students will be able to navigate the teaching portion of the tutorial at their own pace and test their understanding after each step of the lesson with a "Try This" section. The "Try This" section will monitor students answers and self-check by a right answer turning orange and a wrong answer dissolving.

Worksheet

Name Description
Open Number Line:

Open Number Line



Printed On:4/15/2025 7:04:10 PM
Print Page | Close this window