Standard #: MA.5.NSO.1.5


This document was generated on CPALMS - www.cpalms.org



Round multi-digit numbers with decimals to the thousandths to the nearest hundredth, tenth or whole number.


Examples


The number 18.507 rounded to the nearest tenth is 18.5 and to the nearest hundredth is 18.51.

General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 5
Strand: Number Sense and Operations
Standard: Understand the place value of multi-digit numbers with decimals to the thousandths place.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • NA

 

Vertical Alignment

Previous Benchmarks

 

Next Benchmarks

 

Purpose and Instructional Strategies

The purpose of this benchmark is for students to think about the magnitude of multi-digit numbers with decimals to round them to the nearest hundredth, tenth or whole number. In grade 5, the expectations for rounding are to the nearest hundredth and to digits other than the leading digit, e.g., round 29.834 to the nearest hundredth. Students have experience rounding whole numbers to any place in grade 4 (MA.4.NSO.1.4). Rounding skills continue to be important in later grades as students solve real-world problems with fractions and decimals (MA.6.NSO.2.3) and work with scientific notation (MA.8.NSO.1.4). 
  • Instruction develops some efficient rules for rounding fluently by building from the basic strategy of – “Is 29.834 closer to 20 or 30?” Number lines are effective tools for this type of thinking and help students relate the placement of numbers to benchmarks for rounding (MTR.3.1, MTR.5.1). 
  • The expectation is that students have a deep understanding of place value and number sense in order to develop and use an algorithm or procedure for rounding. Additionally, students should explain and reason about their answers when they round and have numerous experiences using a number line and a hundred chart as tools to support their work with rounding.

 

Common Misconceptions or Errors

  • Students may confuse benchmarks by which numbers can round. 
    • For example, when rounding 29.834 to the nearest tenth, they may confuse that the benchmarks are 29.8 and 29.9. The reliance on mnemonics, songs or rhymes during instruction can often confuse students further because it may replace their motivation to think about the benchmark numbers.

 

Strategies to Support Tiered Instruction

  • Instruction includes using number lines and place value understanding to round multi- digit numbers with decimals to the nearest tenth or whole number. 
  • For example, students round 16.32 to the nearest tenth using a number line and place value understanding. The teacher explains that the endpoints of the number line will be represented using tenths, because we are rounding to the nearest tenth. The teacher explains that there are three tenths in the number 16.32 and one more tenth would be four tenths. The teacher represents these endpoints on the number line as sixteen and three-tenths (16.3) and sixteen and four-tenths (16.4) while reminding students that 16.3 is equivalent to 16.30 and 16.4 is equivalent to 16.40. Additionally, the teacher explains that the mid-point on the number line can be labeled as sixteen and three-tenths, five-hundredths or sixteen and 35 hundredths (16.35). This midpoint is halfway between 16.3 and 16.4. The teacher asks students to plot 16.32 on the number line and discuss if it is closer to 16.3 or 16.4, explaining that 16.32 rounds to 16.3 because it is less than the midpoint of 16.35 and closer to 16.3 on the number line. 

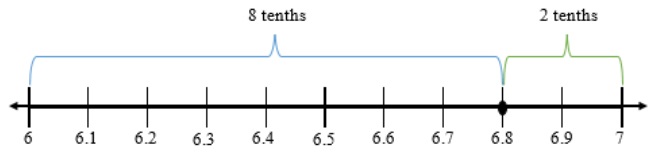
  • For example, students round 6.8 to the nearest whole number using a number line and place value understanding. The teacher explains that the endpoints of our number line will be represented using ones, because we are rounding to the nearest whole number. Also, the teacher explains that there are six ones in the number 6.8 and one more one would be seven ones. The teacher represents these endpoints on the number line as six ones (6) and seven ones (7). The midpoint on the number line is labeled as 6 ones and 5 tenths (6.5). This midpoint is halfway between 6 and 7. The teacher asks students to plot 6.8 on the number line and discuss if it is closer to six or seven, explaining that 6.8 rounds to seven because it is eight-tenths away from six and only two-tenths away from seven. It is also less than the midpoint of 6.5.

 

Instructional Tasks

Instructional Task 1 (MTR.3.1, MTR.6.1) 

Round 29.834 to the nearest whole number. Identify between which two whole numbers 29.834 lies on a number line. 

 

Instructional Task 2 (MTR.3.1, MTR.6.1) 

Round 29.834 to the nearest tenth. Identify between which two tenths 29.834 lies on a number line. 

 

Instructional Task 3 (MTR.3.1, MTR.6.1) 

Round 29.834 to the nearest hundredths. Identify between which two hundredths 29.834 lies on a number line.

 

Instructional Items

Instructional Item 1 

Which of the following are true about the number 104.029? 
  • a. 104.029 rounded to the nearest whole number is 4. 
  • b. 104.029 rounded to the nearest whole number is 104. 
  • c. 104.029 rounded to the nearest tenth is 104.2. 
  • d. 104.029 rounded to the nearest hundredths is 104.02. 
  • e. 104.029 rounded to the nearest hundredths is 104.03. 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.



Related Courses

Course Number1111 Course Title222
5012070: Grade Five Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7712060: Access Mathematics Grade 5 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012065: Grade 4 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))
5012015: Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.5.NSO.1.AP.5 5 Round multi-digit numbers with decimals to the tenths to the nearest whole number (e.g., 1.7 rounds to 2); and numbers with decimals to the hundredths to the nearest tenth (e.g., 2.36 rounds to 2.4). Multi-digit numbers not to exceed 9.99.


Related Resources

Formative Assessments

Name Description
Rounding To The Nearest Whole Number

Students are given four numbers and asked to round each to the nearest whole number and to explain their reasoning.

Rounding To The Thousandths Place

Students are given four numbers and asked to round each to the nearest thousandth and to explain their reasoning.

 

Note: Three of the numbers are decimals to the ten-thousandths place and one number is to the hundred-thousandths place. If students are not ready for rounding larger decimals to the thousandths place, use an alternate MFAS task that rounds to the hundredths, tenths, or whole number.

Rounding To The Tenths Place

Students are given four numbers and asked to round each to the nearest tenth and to explain their reasoning.

Shopping for Produce

Students are asked to round numbers given in a context to the nearest hundredth.

 

Note: The decimals students are rounding in this task extend past the thousandths place. If students are not ready for rounding larger decimals to the hundredths place, use an alternate MFAS task that rounds to the hundredths, tenths, or whole number.

Lesson Plans

Name Description
Beach on a Budget

In this Model Eliciting Activity, MEA, students work in teams to determine which store the client should use to buy beach equipment for a new beach rental business, after considering quality, replacement efficiency, and estimating the total price. After the students have created a proposal based on given data, a twist is added which may vary their results.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

Which Cell Phone for Mia?

In this Model Eliciting Activity, MEA, students help a 5th grader to decide which cell phone she will ask for as a birthday present. Students must use a chart to analyze information and make conclusions based upon their own ranking system within their cooperative group. They then must write a letter to the student justifying their conclusions.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.

Currency Craze!

If I travel to Italy, can I buy a raspberry gelato with a $5.00 bill? Students will understand that other countries use currencies different from the United States, and that when visiting those countries, exchange rates are used to determine the value of the United States dollar (USD). This lesson integrates Mathematics with Social Studies as the students apply their knowledge of decimals and basic operations with their passports for a real-world application.

Estimating Decimal Products

In this lesson, students will learn to estimate decimal products using different strategies to arrive at compatible numbers. They will learn that estimates will vary depending on the strategy chosen and that the closer the compatible numbers are to the actual factors, the closer the estimate will be to the exact answer. Students will also learn that estimation is used to solve problems that don't require exact answers and to check exact answers for reasonableness.

The 20 Second Game

This is a game students will love to play to improve their understanding of estimating decimal products and increase speed when finding these estimations. The game can be modified to practice estimating products of whole numbers, quotients of whole numbers, and quotients of decimals.

Original Student Tutorial

Name Description
Rounding Race

Explore rounding decimals through the thousandths place as you help Tyrese the Turtle train to race the hare in this interactive tutorial.

Perspectives Video: Teaching Idea

Name Description
Precision of Measurement <p>Classroom activities that teach students precision of measurement.</p>

Worksheet

Name Description
Open Number Line

Open Number Line

Student Resources

Original Student Tutorial

Name Description
Rounding Race:

Explore rounding decimals through the thousandths place as you help Tyrese the Turtle train to race the hare in this interactive tutorial.

Worksheet

Name Description
Open Number Line:

Open Number Line



Parent Resources

Worksheet

Name Description
Open Number Line:

Open Number Line



Printed On:4/16/2025 12:28:49 AM
Print Page | Close this window