Solve real-world problems involving addition and subtraction of fractions with like denominators, including mixed numbers and fractions greater than one.
Examples
Example: Megan is making pies and uses the equation
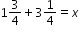
when baking. Describe a situation that can represent this equation.
Example: Clay is running a 10K race. So far, he has run 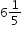 kilometers. How many kilometers does he have remaining?
kilometers. How many kilometers does he have remaining?
Clarifications
Clarification 1: Problems include creating real-world situations based on an equation or representing a real-world problem with a visual model or equation.
Clarification 2: Fractions within problems must reference the same whole.
Clarification 3: Within this benchmark, the expectation is not to simplify or use lowest terms.
Clarification 4: Denominators limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
Subject Area: Mathematics (B.E.S.T.)
Grade: 4
Strand: Algebraic Reasoning
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is to connect procedures for adding and subtracting fractions with like denominators (
MA.4.FR.2.2) to real-world situations. This builds on composing and decomposing fractions (
MA.4.FR.2.1) to connect to addition and subtraction of fractions.
- Instruction should include providing students with the opportunity to recognize models or equations based on a real-world situation.
- Models may include fraction bars, fraction circles, and relationship rods.
- Instruction should include allowing students to create world situations based on models or equations.
- Instruction should include having students connect adding and subtracting procedures to
real-world situations.
Common Misconceptions or Errors
- Students tend to have trouble with addition and subtraction because much instruction focuses only on procedures. Students need to know how to treat the numerator and denominator when following the procedures to add and subtract. It is important for students to use models so they make sense of equations and real-world problems when they solve them.
Strategies to Support Tiered Instruction
- Instruction includes opportunities to engage in teacher-directed practice using visual representations to solve real-world problems involving addition and subtraction of fractions with like denominators. Students use models or equations based on real-world situations with an emphasis on how to treat the numerator and denominator when adding and subtracting.
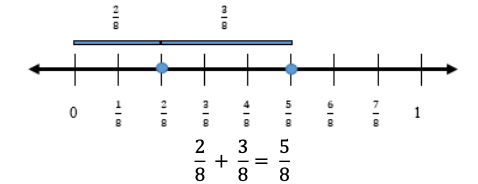
- For example, the teacher displays and reads the following problem: “ Sara read of her book on Friday. On Saturday, she read of her book. How much of her
book did she read on both days combined?” Using a number line, the teacher models solving this problem with explicit instruction and guided questioning. Students explain how to use the number line as a model to solve this question. Have students use an equation to represent the problem. This is repeated with similar real-world problems.
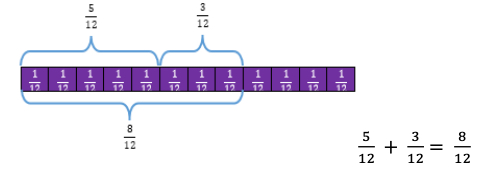
- For example, the teacher displays and reads the following problem: “ Jamal has a raised bed garden in his backyard. He planted tomatoes in of his garden and zucchini in of his garden. What fraction of his garden contains tomatoes and
zucchini?” Using fraction bars or fraction strips, the teacher models solving this problem with explicit instruction and guided questioning. Students explain how to use fraction bars or fraction strips as a model to solve this question and create an equation to represent the problem. This is repeated with similar real-world problems.
Instructional Tasks
Instructional Task 1 (MTR.4.1)
Solve the following problem. Anna Marie has
of a medium cheese pizza. Kent gives her
of a medium pepperoni pizza. How much pizza does Anna Marie have now?
Anna Marie has of a medium pizza. Kent gives her of a large pizza. How much pizza
does Anna Marie have now?
Explain why this problem cannot be solved by adding
+
.
Instructional Items
Instructional Item 1
Jose was completing an exercise program.
of the exercise program was pull-ups. What fraction of the exercise program was not pull-ups?
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
| Course Number1111 |
Course Title222 |
| 5012060: | Grade Four Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7712050: | Access Mathematics Grade 4 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current)) |
| 5012055: | Grade 3 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 5012015: | Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current)) |
Related Access Points
| Access Point Number |
Access Point Title |
| MA.4.AR.1.AP.2 | Solve one-step real-world problems involving addition and subtraction of fractions less than one with like denominators. Denominators limited to 2, 3, 4, 6, 8 or 10. |
Related Resources
Formative Assessment
| Name |
Description |
| Anna Marie and the Pizza | Students are asked to solve a word problem that involves adding fractions with like denominators. Students then analyze a word problem involving addition of unlike unit quantities. |
Lesson Plans
| Name |
Description |
| Learning to Love Like Denominators | Students engage in problem solving to explore the addition and subtraction of fractions with like denominators. Students make sense of the structure of addition and subtraction equations with like denominators and make generalizations to move from using manipulatives, pictures and number lines to simply adding or subtracting the numerator. |
| Adding and Subtracting in the Real World with Unit Fractions | Students will use unit fractions, and counting on or back by unit fractions, to solve addition and subtraction real world problems. |
| Marshmallow Math | In this lesson, students are physically engaged in measuring distances of tossed marshmallows to the nearest 1/2 foot. Using their measurements, they will represent the data on a line plot and then solve word problems involving addition and subtraction of mixed numbers. This is a fun lesson that motivates students to become excited about the difficult world of fractions. |
Perspectives Video: Teaching Idea
Problem-Solving Tasks
| Name |
Description |
| Comparing two different pizzas | The focus of this task is on understanding that fractions, in an explicit context, are fractions of a specific whole. In this this problem there are three different wholes: the medium pizza, the large pizza, and the two pizzas taken together. This task is best suited for instruction. Students can practice explaining their reasoning to each other in pairs or as part of a whole group discussion. |
| Peaches | This task provides a context where it is appropriate for students to subtract fractions with a common denominator; it could be used for either assessment or instructional purposes. For this particular task, teachers should anticipate two types of solution approaches: one where students subtract the whole numbers and the fractions separately and one where students convert the mixed numbers to improper fractions and then proceed to subtract. |
| Plastic Building Blocks | The purpose of this task is to have students add mixed numbers with like denominators. This task illustrates the different kinds of solution approaches students might take to such a task. Two general approaches should be anticipated: one where students calculate exactly how many buckets of blocks the boys have to determine an answer, and one where students compare the given numbers to benchmark numbers. |
Tutorials
Student Resources
Problem-Solving Tasks
| Name |
Description |
| Comparing two different pizzas: | The focus of this task is on understanding that fractions, in an explicit context, are fractions of a specific whole. In this this problem there are three different wholes: the medium pizza, the large pizza, and the two pizzas taken together. This task is best suited for instruction. Students can practice explaining their reasoning to each other in pairs or as part of a whole group discussion. |
| Peaches: | This task provides a context where it is appropriate for students to subtract fractions with a common denominator; it could be used for either assessment or instructional purposes. For this particular task, teachers should anticipate two types of solution approaches: one where students subtract the whole numbers and the fractions separately and one where students convert the mixed numbers to improper fractions and then proceed to subtract. |
| Plastic Building Blocks: | The purpose of this task is to have students add mixed numbers with like denominators. This task illustrates the different kinds of solution approaches students might take to such a task. Two general approaches should be anticipated: one where students calculate exactly how many buckets of blocks the boys have to determine an answer, and one where students compare the given numbers to benchmark numbers. |
Tutorials
Parent Resources
Problem-Solving Tasks
| Name |
Description |
| Comparing two different pizzas: | The focus of this task is on understanding that fractions, in an explicit context, are fractions of a specific whole. In this this problem there are three different wholes: the medium pizza, the large pizza, and the two pizzas taken together. This task is best suited for instruction. Students can practice explaining their reasoning to each other in pairs or as part of a whole group discussion. |
| Peaches: | This task provides a context where it is appropriate for students to subtract fractions with a common denominator; it could be used for either assessment or instructional purposes. For this particular task, teachers should anticipate two types of solution approaches: one where students subtract the whole numbers and the fractions separately and one where students convert the mixed numbers to improper fractions and then proceed to subtract. |
| Plastic Building Blocks: | The purpose of this task is to have students add mixed numbers with like denominators. This task illustrates the different kinds of solution approaches students might take to such a task. Two general approaches should be anticipated: one where students calculate exactly how many buckets of blocks the boys have to determine an answer, and one where students compare the given numbers to benchmark numbers. |


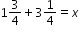 when baking. Describe a situation that can represent this equation.
when baking. Describe a situation that can represent this equation. 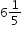 kilometers. How many kilometers does he have remaining?
kilometers. How many kilometers does he have remaining?