Standard #: MA.4.FR.1.3

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.4.FR.2.1
• MA.4.FR.2.3
• MA.4.M.1.1
• MA.4.M.1.2 
• MA.4.DP.1.1
• MA.4.DP.1.2

 

Terms from the K-12 Glossary

• NA

 

Vertical Alignment

Previous Benchmarks

• MA.3.FR.2.2

 

Next Benchmarks

• MA.5.FR.2.1

 

Purpose and Instructional Strategies

The purpose of this benchmark is for students to begin generating equivalent fractions. This work builds on identifying equivalent fractions in grade 3 (MA.3.FR.2.2) and builds the foundation for adding and subtracting fractions with unlike denominators in grade 5 (MA.5.FR.2.1).

• For instruction, students should use multiple models to develop an understanding of equivalent fractions (MTR.2.1). Students can use area models, set models, number lines, and equations to determine and generate equivalent fractions. 
  • Area Model 

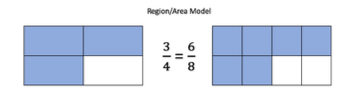
• Number Lines 

• Instruction should focus on reasoning about how the numerator and denominators are affected when equivalent fractions are generated. 
• Reasoning about the size of a fraction using benchmark fractions helps solidify students’ understanding of the size of the fraction. 
• Instruction includes fractions equal to and greater than one.

 

Common Misconceptions or Errors

• Students may think that when generating equivalent fractions, they need to multiply or divide only the numerator or only denominator, such as changing $\frac{\text{3}}{\text{4}}$ to $\frac{\text{3}}{\text{8}}$. 

 

Strategies to Support Tiered Instruction

• Instruction includes opportunities to use concrete models and drawings to solidify understanding of fraction equivalence. Students use models to describe why fractions are equivalent or not equivalent when referring to the same size whole.
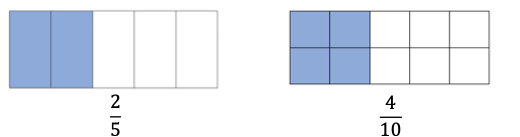
  • For example, when looking at $\frac{\text{2}}{\text{5}}$ and $\frac{\text{4}}{\text{10}}$, conversation includes that both fraction models are the same size. So, when comparing them, we are comparing the same size whole. Students should be able to see that 2 out of the 5 are shaded in the first model and 4 out of the 10 are shaded in the second model, making the $\frac{\text{2}}{\text{5}}$ equal to $\frac{\text{4}}{\text{10}}$. 

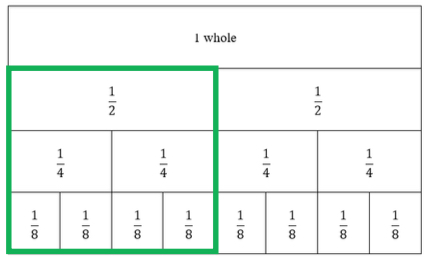
• Instruction includes fraction tiles or fraction kits to physically place and see equivalent fractions of a model. Students line up fraction tiles and begin to make observations about equivalence. One-half is equivalent to 2 one-fourth pieces. Students then notice that those pieces are equivalent to 4 one-eighth pieces. Once students have this understanding, then they can begin to rename fractions.
  • Example:

 

Instructional Tasks

Instructional Task 1 (MTR.4.1) 

Divide the number line below into enough equal sections so that you can locate and label the point $\frac{\text{2}}{\text{5}}$. Divide the same number line with a different color so that you can locate and label the point $\frac{\text{4}}{\text{10}}$. Discuss what you have learned.

 

Instructional Items

Instructional Item 1 

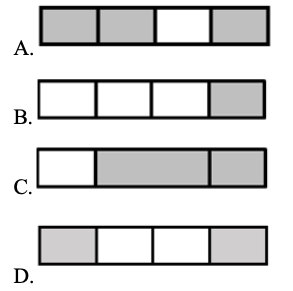
Olivia modeled a fraction by shading parts of the rectangle as shown.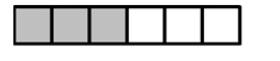 
Ethan draws a rectangle with the same size to model a fraction equivalent to Olivia’s. Which rectangle could Ethan have drawn? 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.