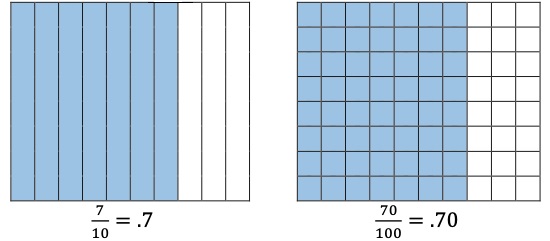
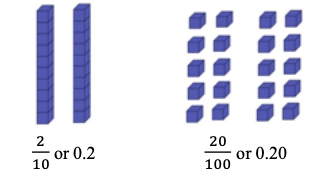
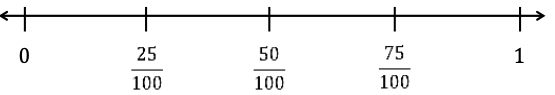Use decimal notation to represent fractions with denominators of 10 or 100, including mixed numbers and fractions greater than 1, and use fractional notation with denominators of 10 or 100 to represent decimals.
Instruction emphasizes conceptual understanding through the use of manipulatives visual models, number lines or equations.
| Name |
Description |
| Cookies, Fractions and Decimals, Oh My! | This lesson asks students to recommend which cookie the owners of The Cookie Jar should add to their menu. Before they make their decision, the students have to convert decimal notation and fractions with denominators 10 and 100 to fractions with like denominators. Then they will be able to see exactly how many people voted for each cookie and they can factor in that information along with additional cookie facts to make their final recommendation.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx |
| Donuts and Decimals | In this MEA, students will convert fractions into decimals and then compare the decimals to decide which donut a donut shop should add to their menu.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx |
| Wondrous Water Parks | This activity requires students to apply their knowledge of unit conversions, speed calculation, and comparing fractions to solve the problem of which water park their class should choose to go on for their 5th grade class trip. |
| Cookies and Treats | Fourth graders will help Cookies and Treats find cost-effective and eco-friendly packaging for its cookies. Students will organize data and compare prices using decimal notation in order to develop a procedure for choosing packaging for cookies. Students will use multiplication and division of whole numbers to plan for how many packages to order. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Equivalency Detectives: Fractions and Decimals! | This is a lesson intended to reinforce students' ability to find equivalent fractions and decimals. The lesson requires prior essential vocabulary knowledge, and a basic understanding of converting fractions to decimals and decimals to fractions (tenths and hundredths). |
| Fractions Undercover! | Students will correctly model and discover fractions and their decimal equivalents through the use of decimal grids and base ten blocks. |
| Dynamic Decimals, Fractions and Money! | This lesson is a practice lesson for student’s knowledge on connecting decimals, money and fractions. |
| Fraction Measuring With Cuisenaire Rods | In this lesson, students will use Cuisenaire rods to measure lengths and generate equivalent fractions. This is a concrete way to introduce how to generate equivalent fractions by finding patterns in the numerators and denominators. |
| Happy Hundredths (Lesson 2 of 2) | In this lesson, students will work with math manipulatives to understand that it takes 100 hundredths of something to make one whole. They will use manipulatives with money (pennies and dollars), fractions (one hundredth pieces and one whole pieces), and base ten blocks (units and wholes) to show different values. They will express values with combinations of the given manipulatives and draw their solutions.
This lesson 2 of 2 in a unit on fraction and decimal concepts |
| Terrific Tenths (Lesson 1 of 2) | Students will work with math manipulatives to understand that it takes 10 tenths to make one whole. They will use manipulatives with money (dimes), fractions (one tenth pieces), and base ten blocks (rods) to show different values. They will use decimal notation to record these tenths.
This is lesson one in a two part lesson unit. Lesson two (HAPPY HUNDREDTHS) deals with hundredths. |
| Name |
Description |
| How Many Tenths and Hundredths? | The purpose of this task is for students to finish the equations to make true statements. Parts (a) and (b) have the same solution, which emphasizes that the order in which we add doesn't matter (because addition is commutative), while parts (c) and (d) emphasize that the position of a digit in a decimal number is critical. The student must really think to encode the quantity in positional notation. In parts (e), (f), and (g), the base-ten units in 14 hundredths are bundled in different ways. In part (e), "hundredths" are thought of as units: 14 things = 10 things + 4 things. Part (h) addresses the notion of equivalence between hundredths and tenths. |
| Expanded Fractions and Decimals | The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit. |
| Dimes and Pennies | The purpose of this task is to help students gain a better understanding of fractions through the use of dimes and pennies. |
| Name |
Description |
| How Many Tenths and Hundredths?: | The purpose of this task is for students to finish the equations to make true statements. Parts (a) and (b) have the same solution, which emphasizes that the order in which we add doesn't matter (because addition is commutative), while parts (c) and (d) emphasize that the position of a digit in a decimal number is critical. The student must really think to encode the quantity in positional notation. In parts (e), (f), and (g), the base-ten units in 14 hundredths are bundled in different ways. In part (e), "hundredths" are thought of as units: 14 things = 10 things + 4 things. Part (h) addresses the notion of equivalence between hundredths and tenths. |
| Expanded Fractions and Decimals: | The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit. |
| Dimes and Pennies: | The purpose of this task is to help students gain a better understanding of fractions through the use of dimes and pennies. |
| Name |
Description |
| How Many Tenths and Hundredths?: | The purpose of this task is for students to finish the equations to make true statements. Parts (a) and (b) have the same solution, which emphasizes that the order in which we add doesn't matter (because addition is commutative), while parts (c) and (d) emphasize that the position of a digit in a decimal number is critical. The student must really think to encode the quantity in positional notation. In parts (e), (f), and (g), the base-ten units in 14 hundredths are bundled in different ways. In part (e), "hundredths" are thought of as units: 14 things = 10 things + 4 things. Part (h) addresses the notion of equivalence between hundredths and tenths. |
| Expanded Fractions and Decimals: | The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit. |
| Dimes and Pennies: | The purpose of this task is to help students gain a better understanding of fractions through the use of dimes and pennies. |