Standard #: MA.4.FR.1.1

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.4.NSO.2.6
• MA.4.NSO.2.7 
• MA.4.FR.2.3

 

Terms from the K-12 Glossary

• NA

 

Vertical Alignment

Previous Benchmarks

• MA.3.FR.2.2

 

Next Benchmarks

• MA.5.FR.2.1

 

Purpose and Instructional Strategies

The purpose of this benchmark is to have students begin connecting fractions with decimals. This benchmark will connect fractions and decimals by writing equivalent fractions with denominators of 10 or 100 (decimal fractions). Decimal fractions are defined as fractions with denominators of a power of ten. 

• For students to have a concrete foundation for future work with decimals (MA.4.NSO.1.5, MA.4.FR.1.2, MA.4.FR.1.3), plan experiences that allow students to use 10 by 10 grids, base-ten blocks, and other place value models (MTR.2.1) to explore the relationship between fractions with denominators of 10 and denominators of 100. 
• This work lays the foundation for performing decimal addition and subtraction in MA.4.NSO.2.7.

 

Common Misconceptions or Errors

• Students often confuse decimals such as 0.6 and 0.06. Students need to have a conceptual understanding of the visual representations for tenths and hundredths. Students should use models and explain their reasoning to develop their understanding of the connections between fractions and decimals.

 

Strategies to Support Tiered Instruction

• Instruction includes concrete models and drawings to solidify the conceptual understanding of fraction place value. 
• For example, students create a model for $\frac{\text{2}}{\text{10}}$. The teacher then asks students to model a fraction that is equivalent to a denominator of 100 and explain what they notice about the models. Conversation involves connections to the value of the fractions. 

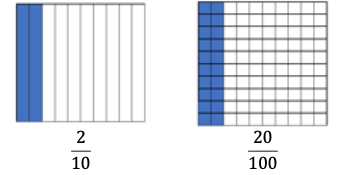
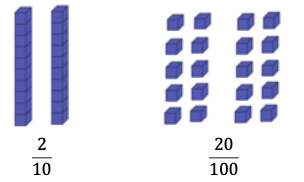
• Instruction includes building fractions and their equivalents with base ten blocks. 
  • For example, students build $\frac{\text{2}}{\text{10}}$ “two-tenths” and $\frac{\text{20}}{\text{100}}$“ twenty hundredths” with base ten blocks while using vocabulary that will help students see the decimal connection as well. Students will realize that the numbers have the same value. 

• Instruction includes opportunities to use concrete models and drawings to solidify understanding of fraction equivalence. 
  • For example, students use models to describe why fractions are equivalent or not equivalent when referring to the same size whole. 

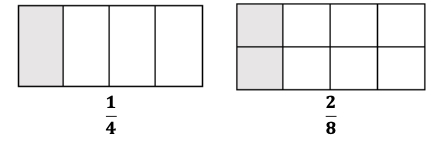
• When looking at $\frac{\text{1}}{\text{4}}$ and $\frac{\text{2}}{\text{8}}$, discussion includes that both fraction models are the same size. So, when comparing them, we are comparing the same size whole. Students see that 1 out of the 4 are shaded in the first model and 2 out of the 8 are 2 are shaded in the second model, making the $\frac{\text{1}}{\text{4}}$ equal $\frac{\text{2}}{\text{8}}$. Students use this understanding to move into fractions with larger denominators.

 

Instructional Tasks

Instructional Task 1 (MTR.4.1) 

Shade the models to complete the equivalent fractions.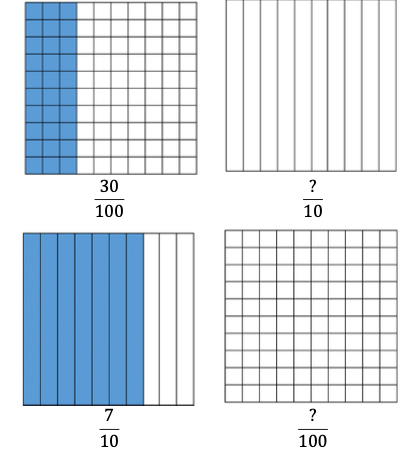

 

Instructional Items

Instructional Item 1 

An equation is shown. What number completes the equivalent fraction?  

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.