General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 4
Strand: Number Sense and Operations
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Expression
- Equation
- Factor
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
- The purpose of this benchmark is for students to become procedurally fluent in using a standard algorithm. Work with standard algorithms began in the procedural reliability stage when students explored a variety of methods and learned to use at least one of those methods accurately and reliably.
- It is important to challenge students to explain the steps they follow when using a standard algorithm (i.e. regrouping, proper recording, and placement of digits by place value).
Common Misconceptions or Errors
- Students that are taught a standard algorithm without any conceptual understanding will often make mistakes. For students to understand a standard algorithm or any other method, they need to be able to explain the process of the method they chose and why it works. This explanation may include pictures, properties of multiplication, decomposition, etc.
- Some students may struggle with this benchmark if they do not have a strong command of basic addition and multiplication facts.
Strategies to Support Tiered Instruction
- Instruction includes explaining mathematical reasoning while using a multiplication algorithm. Instruction also includes determining if an algorithm was used correctly by reviewing the reasonableness of solutions.
- For example, students use an algorithm to determine 41 × 23 and explain their thinking using place value understanding. Explicit instruction includes: “Begin by multiplying 3 ones times 1 one. This equals 3 ones. We will write the 3 ones under the line, in the ones place. Next, we will multiply 3 ones times 4 tens. This equals 12 tens. We will write the 12 tens under the line in the hundreds and tens place because 12 tens is the same as 1 hundred and 2 tens. This gives us our first partial product of 123. Now we will multiply the 1 one by the 2 tens from 23. This equals 2 tens or 20. We will record 20 below our first partial product of 123. Next, we, we will multiply 2 tens times 4 tens, which equals 8 hundreds. We will write the 8 in the hundreds place of our second partial product. Our second partial product is 820. Finally, we add our partial products to find the product of 943.”
- For example, students determine 41 × 23 using an area model and place value understanding.
- For example, students use an algorithm to determine 4 × 36 and explain their thinking using place value understanding. Instruction includes stating, “Begin by multiplying 4 ones times 6 ones. This equals 24 ones or 2 tens and 4 ones. We will write the 4 ones from 24 under the line, in the one's place. We will write the 2 tens from 24 as a 2 above the 3, as a regrouped digit in the tens place. Next, we will multiply 4 ones times 3 tens. This equals 12 tens. We will add the 2 tens to the 12 tens for a total of 14 tens. We will write the 14 tens under the line in the hundreds and tens place because 14 tens is the same as 1 hundred and 4 tens. Our product is 144.”
- For example, students determine 4 × 36 using an area model and place value understanding.
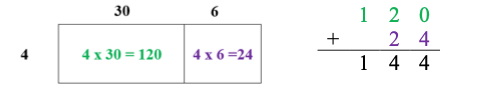
- Instruction includes the use of known facts to find unknown multiplication facts.
- For example, if the student does not know the product for 4 × 6 from the previous 120 +24 144 example, have students use a known fact such as 4 × 5. The known fact of 4 × 5 = 20 can be used to find the product of 4 × 6 by adding one more group of 4 to the product of 20 to find the product of 24.
Instructional Tasks
Instructional Task 1 (MTR.4.1, MTR.5.1)
Using the digits 1, 2, 3 and 4, arrange them to create two 2-digit numbers that when multiplied, will yield the greatest product.
Instructional Items
Instructional Item 1
Select the expressions that have a product of 480.- a. 10×48
- b. 16×30
- c. 24×24
- d. 32×15
- e. 40×80
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.