Standard #: MA.4.NSO.1.5

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.4.NSO.2.6
• MA.4.NSO.2.7 
• MA.4.FR.1.2
• MA.4.FR.1.4 
• MA.4.DP.1.1
• MA.4.DP.1.3

 

Terms from the K-12 Glossary

• NA

 

Vertical Alignment

Previous Benchmarks

• MA.3.NSO.1.3

 

Next Benchmarks

• MA.5.NSO.1.4

 

Purpose and Instructional Strategies

The purpose of this benchmark is for students to plot, order, and compare decimals using place value. Grade 4 contains the first work with decimals. During instruction make connections to decimal fractions (e.g.,$\frac{\text{1}}{\text{10}}$, $\frac{\text{1}}{\text{100}}$) (MA.4.FR.1.2). 

• For instruction, teachers should show students how to represent these decimals on scaled number lines. Students should use place value understanding to make comparisons. 
• Students learn that the names for decimals match their fraction equivalents (e.g., 2 tenths is equivalent to 0.2 which is equivalent to $\frac{\text{2}}{\text{10}}$). 
• Students build area models (e.g., a 10 × 10 grid) and other models to compare decimals.

 

Common Misconceptions or Errors

• Students treat decimals as whole numbers when making a comparison of two decimals. They think the longer the number, the greater the value. 
  • For example, they think that 0.04 is greater than 0.4.

 

Strategies to Support Tiered Instruction

• Instruction includes the use of place value understanding, decimal fractions, and decimal grids to compare decimals. 
  • For example, students compare 0.14 and 0.2 using decimal fractions. The teacher begins instruction by having students write each decimal as a fraction, $\frac{\text{14}}{\text{100}}$ and $\frac{\text{2}}{\text{10}}$. The teacher explains that $\frac{\text{2}}{\text{10}}$ is equal to $\frac{\text{20}}{\text{100}}$ because if we multiply the numerator and denominator of $\frac{\text{2}}{\text{10}}$ by 10, we generate the equivalent fraction $\frac{\text{2}}{\text{10}}$ = $\frac{\text{2x10}}{\text{10x10}}$. Next, the teacher compares the fractions to determine that $\frac{\text{14}}{\text{100}}$ < $\frac{\text{20}}{\text{100}}$ , so 0.14 < 0.2. 
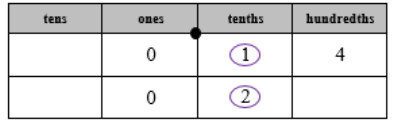
  • For example, students use place value understanding and a place value chart to compare 0.14 and 0.2. The teacher explains that when comparing decimals, we start with the digit to the far left because we want to compare the greatest place values first. Both values have a 0 in the ones place, so we will move to the tenths place. One-tenth is less than two-tenths, so 0.14 < 0.2. 

• For example, students compare 0.3 and 0.03 using decimal fractions. The teacher begins instruction by having students write each decimal as a fraction, $\frac{\text{3}}{\text{10}}$ and $\frac{\text{3}}{\text{100}}$. The teacher then explains to students that $\frac{\text{3}}{\text{10}}$ is equal to $\frac{\text{30}}{\text{100}}$, because if we multiply the numerator and denominator of $\frac{\text{3}}{\text{10}}$ by 10, we generate the equivalent fraction $\frac{\text{3}}{\text{10}}$ = $\frac{\text{3x10}}{\text{10x10}}$. Next, the teacher compares the fraction to determine that $\frac{\text{30}}{\text{100}}$ > $\frac{\text{3}}{\text{100}}$, so 0.3 > 0.03. 
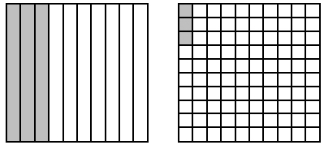
• For example, students compare 0.3 and 0.03 using decimal grids, representing each value, and explain that 0.3 covers a greater area of the decimal grid than 0.03, so 0.3 is greater than 0.03. that 30 > 3 , so 0.3 > 0.03. 

 

Instructional Tasks

Instructional Task 1 (MTR.3.1) 

Use relational symbols to fill in the blanks to compare the numbers. 

• a) 3 tenths + 5 hundredths _____ 3 tenths + 11 hundredths 
• b) 4 hundredths + 5 tenths _____ 1 tenths + 33 hundredths 
• c) 4 hundredths + 1 tenths _____ 1 tenth + 4 hundredths
• d) 5 hundredths + 1 tenth _____ 15 hundredths + 0 tenths 
• e) 5 hundredths + 1 tenth _____ 0 tenths + 15 hundredths

 

Instructional Items

Instructional Item 1

Select all the values that would make the comparison 0.6 > __ a true statement. 

• a. 0.06 
• b. 0.70 
• c. 0.8 
• d. 0.5 
• e. 0.4 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.