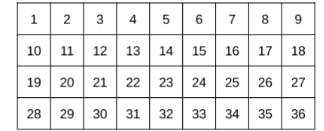
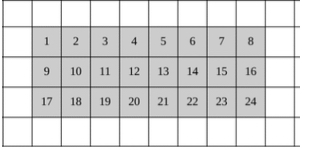
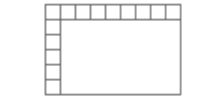
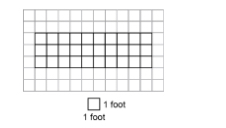
Explore area as an attribute of a two-dimensional figure by covering the figure with unit squares without gaps or overlaps. Find areas of rectangles by counting unit squares.
Instruction emphasizes the conceptual understanding that area is an attribute that can be measured for a two-dimensional figure. The measurement unit for area is the area of a unit square, which is a square with side length of 1 unit.
| Name |
Description |
| Complete the Rectangle | Students are given a rectangle with one column and one row of unit squares (same size squares) drawn. Students are asked to complete and then find the total number of same size squares in the partition. |
| How Many Units? | Students are given a rectangle with some columns and rows partially constructed. Students are asked to find how many same-size squares are in the rectangle. |
| Construct Rows and Columns | Students are given a rectangle with tick marks drawn horizontally on one side of the rectangle and vertically on the bottom of the rectangle. Students are asked to partition the rectangle into columns and rows and then determine how many unit squares (same-size squares) are in the rectangle. |
| Partition the Rectangle Into Unit Squares | Students are given a rectangle with one unit square (same size square) drawn in the corner of the rectangle. Students are asked to draw the remaining unit squares and then find the total number of unit squares in the rectangle. |
| Using Tiles of Different Sizes | Students consider whether tiling a rectangle with different sized tiles is appropriate when calculating area. |
| Unit Square | Students are asked to explain how the area of a rectangle can be calculated and their responses are examined for references to the unit square as the unit of measurement. |
| Overlapping Tiles | Students are asked to evaluate another student's area calculation that involves overlapping tiles. |
| Calculating Area | Students discuss the meaning of area and are asked about the kinds of figures for which area can be calculated. |
| Dawn’s Vegetable Garden | Students are given a diagram showing a garden shaped like an irregular hexagon and are asked to find the area by counting the number of unit squares the figure contains. |
| Area of a Right Trapezoid | Students determine the area of a right trapezoid. |
| How Many Square Units? | Students determine the area of a right triangle. |
| Fenced Dog Run | Students are given a diagram showing a rectangular dog run and asked to find its area. |
| Name |
Description |
| Area Architects, Lesson 1 | In this unit on area, students explore geometric measurement by becoming "Area Architects" in order to learn the concepts of area. Using all five lessons will allow the students to discover, explore and eventually relate area to multiplication and addition. This lesson is the first lesson of the unit. In Lesson 1, students will develop strategies for finding area by counting square units. Students will learn the importance of accurately measuring area by exploring the concepts of area in realistic applications. |
| From Arrays to Areas | Students will be asked to use different strategies to figure out the area of rectangles.. Students progress from playing a game with arrays, to creating rectangles with square tiles, and finally to exploring the area formula. |
| All About Area | This lesson is an introductory lesson about area at the third-grade level. Students will play a game to learn the definition of area, build with square tiles to discover we measure area with square units, and then put this knowledge in practice to complete two worksheets. |
| Best Vegetable Garden | The students will plan a vegetable garden, deciding which kinds of vegetables to plant, how many plants of each kind will fit, and where each plant will be planted in a fixed-area garden design. Then they will revise their design based on new garden dimensions and additional plant options. Students will explore the concept of area to plan their garden and they will practice solving 1 and 2-step real-world problems using the four operations to develop their ideas. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Rectangles Rule! (Lesson 1 of 2) | In this lesson students will use rulers to measure the side lengths of rectangles and use 1-inch square tiles to cover the rectangles. Students will count the total number of square units to find the area and explore relationships between the lengths of the sides and the total number of tiles. In # 66132 Rectangles Rule! Team Challenge (Lesson 2 of 2), students will expand their understanding of tiling to find area to connect area to a multiplication formula. |
| Treehouse Makeover MEA | In this Model Eliciting Activity, MEA, The Shady Oak Treehouse Club is doing a makeover and needs help choosing flooring. Students will be asked to figure area, calculate cost, and add installation fees to cost. The students will then rank the flooring and choose the best one for the makeover. The data provided is: a model of the treehouse (in square yards), flooring price per square yard, and ratings for ease of cleaning, comfort, and color choices. In the twist, student will be provided with an installation fee for each flooring material and must decide if, and how, to change their procedure with the new information.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx |
| Same Perimeter, Different Area | In this lesson, students are presented with a problem that requires them to create rectangles with the same perimeter but different areas. Students also search for relationships among the perimeters and areas of different rectangles and find which characteristics produce a rectangle with the greatest area. |
| Which Rectangle is Bigger? | Students will learn how to partition rectangles into equal parts and write equations to represent the parts. They will gain a basic understanding of area from the book Bigger, Better, BEST! by Stuart J. Murphy. |
| Count Those Square Units | Students count unit squares to find the area of rectangles and play a matching game for practice. |
| Field Day Fun | In this Model Eliciting Activity, MEA, students will choose their top choices of field day activities given the area required for event, safety concerns, clean up required, number of students that can play at a time, and peer comments about the activity. Students will need to make trade-offs in cost when the "twist" provides budget restrictions. Students will count unit squares to calculate area, multiply one-digit numbers by multiples of ten, and add multi-digit whole numbers.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx |
| Make A Mighty Monster: Practice with Area and Perimeter | In this lesson, students will use their knowledge of area and perimeter to create a "Mighty Monster”. Given specific criteria related to area and perimeter, students will make their monster on centimeter grid paper and calculate both the area and perimeter of each body part to explore the differences between the two types of measurement. |
| Area Designers | This hands-on lesson makes a real-world connection for students in measuring area by counting square units. Students become area designers during an activity that illustrates area, and then make a real-world connection with area when they are shown a residential blueprint. Students gain practice determining the area and recording the area of rectangular rooms in square units. |
| Area Isn't Just for Squares | This lesson helps students make the connections between area and multiplication using square tiles. |