General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 3
Strand: Algebraic Reasoning
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Expression
- Equation
- Distributive property
- Factors
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to apply what they have learned about the multiplication of one-digit numbers and multiples of ten to then multiply a one-digit number and a two-digit number (MA.3.NSO.2.3).
- Students are introduced to the distributive property of multiplication over addition as a strategy for using products that they know in order to solve products that they do not know. For example, if students are asked to find the product of 6 x 9, they might decompose 6 into 4 and 2 and then multiply 4 x 9 and 2 x 9 to arrive at 36 + 18, which equals 54. Because of the distributive property, students use parentheses to show how to decompose two-digit numbers by the value of their tens and ones, and then multiply the one-digit number by both the values of the two-digit number’s tens and ones values and find the sum of those products. The application of the commutative and associative properties of multiplication allows for two-digit numbers to be decomposed and multiplication expressions reorganized so that the distributive property can work (MTR.2.1).
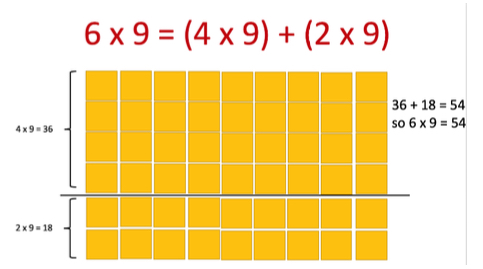
- During instruction, teachers should model where the properties are applied while multiplying and expect students to explain how they work during explanations of their strategies and solutions. Splitting arrays can help students understand the distributive property. They can use a known fact to learn other facts that may cause difficulty (MTR.2.1, MTR.4.1).
- Building understanding of the distributive property in Grade 3 will help students decompose larger numbers as they continue to multiply multi-digit numbers with procedural reliability and procedural fluency in Grade 4. Splitting arrays can help students understand the distributive property. They can use a known fact to learn other facts that may cause difficulty.
Common Misconceptions or Errors
- Students can be confused about how to write expressions using the distributive property. One common mistake that students make is writing an expression 4 × 72 as (4 × 70) × (4 × 2) instead of (4 × 70) + (4 × 2). Instruction should show concrete models (e.g., base ten drawings) along with equations so students can understand the relationship between multiplication and addition while applying the property and writing expressions.
Strategies to Support Tiered Instruction
- Instruction includes opportunities to use concrete models and drawings along with equations to increase understanding of the relationship between multiplication and addition when applying the distributive property and writing equations. The teacher begins by modeling a one-digit number multiplied by a one-digit number, guiding students to decompose one of the factors, and using models or drawings to demonstrate the reorganization of the multiplication expression using parentheses. Next, the teacher models the multiplication of a one-digit number by a two-digit number, guiding students to decompose the two-digit number into the value of the tens and the ones using models or drawings. The teacher clarifies that the decomposed factor can be represented in expanded form by adding the tens and the ones, repeating with additional one-digit by two-digit multiplication equations.
- For example, the teacher uses a model or drawing to use the distributive property to solve 3 x 24.
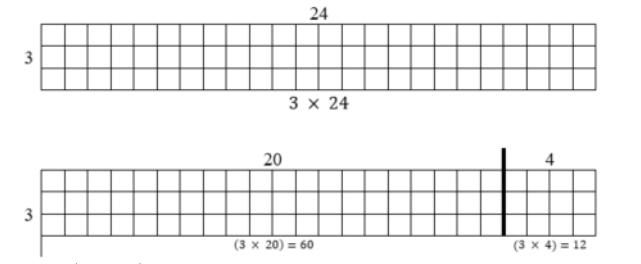
- 3 × (20 + 4)
- (3 × 20) + (3 × 4)
- (3 × 20) + (3 × 4) = 60 + 12
- (3 × 20) + (3 × 4) = 72
so 3 × 24 = 72
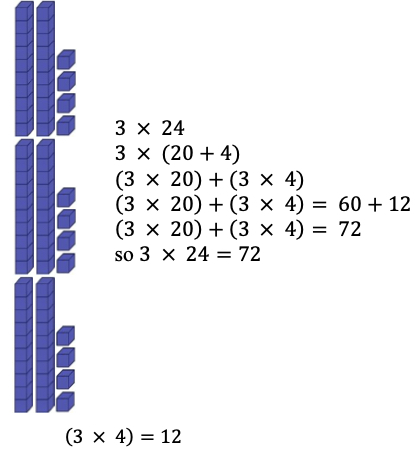
- Teacher provides opportunities to apply the distributive property to solve one-digit by two-digit multiplication equations using base-ten blocks or place value disks. The teacher provides the equation and guides students to decompose the two-digit number into the value of the tens and the ones using manipulatives. If needed, the teacher prompts students to count by 10s and 1s using the base-ten blocks or place value disks.
- For example, the teacher uses base-ten blocks to solve 3 × 24 while asking guiding questions such as “How many tens are in 24?” “How many ones are in 24?” “How would we write 24 in expanded form?”
Instructional Tasks
Instructional Task 1
In each equation, find the missing value, n.
.
- Part A. 4 × 52 = (4 × 50) + (4 × )
- Part B. × 3 = (20 × 3) + (9 × 3)
- Part C. 8 × 36 = ( × 30) + ( × 6)
- Part D. 48 × 6 =
Instructional Task 2
- Tory tried to use the associative and commutative properties to create the following equations. Using pictures and/or words, explain why Tory is incorrect.
- 4 x (11 + 6) = (4 x 11) + 6
- 4 x (11 + 6) = 11 x (4 + 6)
Instructional Items
Instructional Item 1
Which of the following correctly uses the distributive property to multiply 8 × 39 ?
- a. (8 × 30) × (8 × 9) = 24 + 72 = 96
- b. (8 × 30) + (8 × 9) = 240 + 56 = 296
- c. (8 × 30) + (8 × 9) = 38 + 17 = 45
- d. (8 × 30) + (8 × 9) = 240 + 72 = 312