Represent and interpret fractions, including fractions greater than one, in the form of as the result of adding the unit fraction to itself m times.
Examples
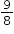
can be represented as
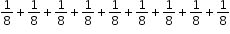
.
Clarifications
Clarification 1: Instruction emphasizes conceptual understanding through the use of manipulatives or visual models, including circle graphs, to represent fractions.
Clarification 2: Denominators are limited to 2, 3, 4, 5, 6, 8, 10 and 12.
Subject Area: Mathematics (B.E.S.T.)
Grade: 3
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to think conceptually about fractions as they plot, compare, order and determine equivalence in Grade 3. It also allows students to develop the counting strategies and additive reasoning required to add and subtract fractions in Grade 4
(MTR.2.1, MTR.5.1). - During instruction, teachers should have students practice representing fractions using manipulatives (e.g., fraction strips, circles, relationship rods), visual area models (e.g., partitioned shapes) and on a number line. Manipulatives, visual models and number lines must extend beyond 1 so that students can represent fractions greater than one (MTR.2.1, MTR.5.1).
- In instruction of MA.3.FR.1.1, students learn that unit fractions are the foundation for all fractions. MA.3.FR.1.2 builds understanding that all fractions, including fractions equal to and greater than one, decompose as the sum of unit fractions.
- In understanding fractions are numbers, students make connections about whole number operations that will allow them to perform operations with fractions in later grades. For
example, understanding fractions as numbers allows students to reason that + = in Grade 4 because we are adding together a total of 4 parts that are each one-third in size (MTR.5.1).
Common Misconceptions or Errors
- Students can misconceive that fractions equal to and greater than 1 can also be represented as the sum of unit fractions (e.g., = + + + + ). Flexible
representations of models (e.g., rectangular area models that align with number lines) help students connect their understanding of fractions and how they are decomposed into unit fractions.
Strategies to Support Tiered Instruction
- Instruction includes modeling how fractions are decomposed. Using fraction circles, students build and then see that there are 4 pieces that make up the whole circle.
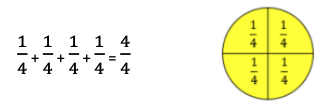
- Instruction includes more than one model so that students can experience and connect fractions in multiple ways. Flexible representations of models (e.g., rectangular area models that align with number lines) help students connect their understanding of fractions and how they are decomposed into unit fractions.
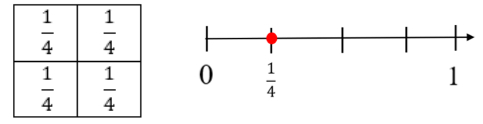
- Students then apply this understanding to fractions greater than one. Using fraction circles, students build and then see that there are 8 pieces that make up
two whole circles.

- Instruction includes folding and/or cutting pre-made shapes into halves. Students physically bend the paper into halves and then label the pieces. Instruction includes relating the pieces back to the numerator and denominator and then connecting it to the equation. Using multiple shapes with the same denominators will solidify basic fraction understanding. Instruction should progress with other denominators.

Instructional Tasks
Instructional Task 1
- Part A. How many one-fifth sized parts are added together to equal 1 whole? Prove your thinking with a visual model or number line.
- Part B. How many one-fifth sized parts are added together to equal 2 wholes? Prove your thinking with a visual model or number line.
Instructional Items
Instructional Item 1
- Represent the fraction 8/3 as the sum of unit fractions.
Instructional Item 2
- Which of the following expressions models 7/4 ?
- c. + + + + + +
- d. + + + + + +
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
| Course Number1111 |
Course Title222 |
| 5012050: | Grade Three Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7712040: | Access Mathematics Grade 3 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current)) |
| 5012055: | Grade 3 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 5012015: | Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current)) |
Related Access Points
| Access Point Number |
Access Point Title |
| MA.3.FR.1.AP.2 | Explore fractions, less than or equal to a whole, in the form of 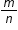 as the result of adding the unit fraction as the result of adding the unit fraction 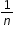 to itself m times. Denominators are limited to 2, 3 and 4. to itself m times. Denominators are limited to 2, 3 and 4. |
Related Resources
Formative Assessments
| Name |
Description |
| Three Quarters Of The Race | Students are read a word problem about a student who has run three-fourths of a race and asked to describe what that means. |
| Painting A Wall | Students are read a word problem about a wall being painted and asked to describe what three-eighths of the wall means. |
| How Many Fourths Are In Two Wholes? | Students are asked to divide two rectangles into fourths and then to consider how many fourths the two wholes represent. |
Image/Photograph
| Name |
Description |
| Clipart ETC Fractions | Illustrations that can be used for teaching and demonstrating fractions. Fractional representations are modeled in wedges of circles ("pieces of pie") and parts of polygons. There are also clipart images of numerical fractions, both proper and improper, from halves to twelfths. Fraction charts and fraction strips found in this collection can be used as manipulatives and are ready to print for classroom use. |
Lesson Plans
| Name |
Description |
| Fraction Action! | This lesson will help students understand that fractions are parts of a whole. The lesson introduces fractional parts using familiar manipulatives. |
| The Human Number Line | In this lesson, students will create a human number line by estimating a fraction's approximate location on the number line between zero and one. This lesson helps students visualize fractions’ relative distance from 0 in order to order and compare fractions and engages them in justifying their thinking. |
| Fraction Name Art | This lesson is designed to introduce and give students practice with the concept of fractions as part of a set. Students will use their classmates to create fraction statements, play a guessing game with color tiles, and finally write fractional statements about their own Name Art! |
| Would You Rather? | This lesson is designed to help students generate rules for comparing fractions. The students will use fraction tiles to discover ways to compare fractions with the same denominator or fractions with the same numerator. They will also begin to use benchmark fractions to help make comparisons and complete inequalities. |
| The "Whole" Deal | In this lesson, students will extend their understanding of unit and non-unit fractions by using different pattern blocks to represent one whole and then determining the fractional part the other pattern blocks represent. |
Original Student Tutorials
Perspectives Video: Teaching Ideas
Virtual Manipulative
| Name |
Description |
| Build a Fraction |
This virtual manipulative will help the students to build fractions from shapes and numbers to earn stars in this fraction lab. To challenge the children there are multiple levels, where they can earn lots of stars.
Some of the sample learning goals can be:
- Build equivalent fractions using numbers and pictures.
- Compare fractions using numbers and patterns
- Recognize equivalent simplified and unsimplified fractions
|
Student Resources
Original Student Tutorials
Virtual Manipulative
| Name |
Description |
| Build a Fraction: |
This virtual manipulative will help the students to build fractions from shapes and numbers to earn stars in this fraction lab. To challenge the children there are multiple levels, where they can earn lots of stars.
Some of the sample learning goals can be:
- Build equivalent fractions using numbers and pictures.
- Compare fractions using numbers and patterns
- Recognize equivalent simplified and unsimplified fractions
|
Parent Resources
Image/Photograph
| Name |
Description |
| Clipart ETC Fractions: | Illustrations that can be used for teaching and demonstrating fractions. Fractional representations are modeled in wedges of circles ("pieces of pie") and parts of polygons. There are also clipart images of numerical fractions, both proper and improper, from halves to twelfths. Fraction charts and fraction strips found in this collection can be used as manipulatives and are ready to print for classroom use. |
Virtual Manipulative
| Name |
Description |
| Build a Fraction: |
This virtual manipulative will help the students to build fractions from shapes and numbers to earn stars in this fraction lab. To challenge the children there are multiple levels, where they can earn lots of stars.
Some of the sample learning goals can be:
- Build equivalent fractions using numbers and pictures.
- Compare fractions using numbers and patterns
- Recognize equivalent simplified and unsimplified fractions
|
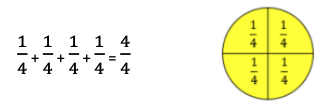




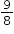 can be represented as
can be represented as 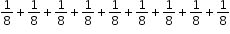 .
.