Standard #: MA.1.AR.1.1


This document was generated on CPALMS - www.cpalms.org



Apply properties of addition to find a sum of three or more whole numbers.  


Examples


8+7+2 is equivalent to 7+8+2 which is equivalent to 7+10 which equals 17.

Clarifications


Clarification 1: Within this benchmark, the expectation is to apply the associative and commutative properties of addition. It is not the expectation to name the properties or use parentheses. Refer to Properties of Operations, Equality and Inequality (Appendix D).

Clarification 2: Instruction includes emphasis on using the properties to make a ten when adding three or more numbers. 

Clarification 3: Addition is limited to sums within 20.



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 1
Strand: Algebraic Reasoning
Standard: Solve addition problems with sums between 0 and 20 and subtraction problems using related facts.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Associative Property of Addition 
  • Commutative Property of Addition 
  • Equation 
  • Expression

 

Vertical Alignment

Previous Benchmarks

 

Next Benchmarks

 

Purpose and Instructional Strategies

The purpose of this benchmark is for students to explore addition and think flexibly when it comes to adding three numbers together such as rearranging addends, looking for doubles, making a ten, etc. In Kindergarten, students find ways to make a ten when given a 1 to 9 digit. Students also find ways to represent a given number from 0 to 10 as the sum of two numbers (MTR.2.1, MTR.5.1). 
  • Instruction includes use of manipulatives to model addition problems within 20 (MTR.5.1).

 

Common Misconceptions or Errors

  • Students may not understand that when three numbers are rearranged the sum will still be the same. In this case, open a class discussion by showing the following expressions A. 3 + 9 + 4 and B. 9 + 4 + 3 and ask students what they notice about the expressions. Once a student notices that they both expressions have the same exact numbers but that the numbers are arranged in a different order ask, “Do you think they will have the same sum?” Have students share how they could solve the expressions using a strategy. Then discuss the sums of both equations being 16 and when one adds the same numbers together but in a different order it will always have the same total.

 

Strategies to Support Tiered Instruction

  • Instruction provides opportunities to use a set of three number cards and make multiple equations with three addends. Students solve all equations and then discuss how they are similar and different. 
    • For example, students choose three numbers from a set of number cards and create the equations below. After students have finished solving the equations, they answer and discuss the following questions: How are the equations different? Students should discuss how the order of the addends is different in each equation. How are the equations the same? Students should conclude that the sum is always the same no matter the order in which the addends are added. Would the same thing happen if we used three different number cards? Would we be able to create equations in which the addends are in different orders? Would the sum be the same no matter the order in which we add the addends? 

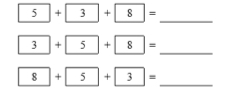
multiple equations with three addends

  • Instruction provides opportunities to build equations with three addends in multiple orders to explore the concept of the commutative property. 
    • For example, the teacher provides the expression 3 + 2 + 4. Students build each addend using snap cubes and determine the sum. Teacher records the student work on chart paper. Teacher gives the students another expression 2 + 4 + 3. Students build each addend using snap cubes and determine the sum. Teacher adds the student work to the chart paper. Teacher gives the students a final expression 4 + 3 + 2. Students build each addend and determine the sum. Teacher adds the students work to the chart paper. Teacher asks “How are these equations similar? How are they different? What do you think would happen if we solved 3 + 4 +2?”

 

Instructional Tasks

Instructional Task 1 (MTR.2.1) 

Provide students with three different colors of manipulatives (six of each color), three dice and a recording sheet. 
  • Part A. Student rolls three dice and set out that many one color manipulatives per die that they rolled. Student arranges the manipulatives to create an addition sentence then records it.
  • Part B. Student rearrange their manipulatives to create a new addition sentence and records it. Student thinks of another way they could get to their sum by creating a true equation. 

 

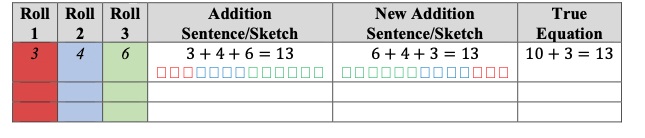
Instructional Task 2 (MTR.5.1, MTR.6.1) 

Melonie is working on solving an addition problem with three numbers. She says that she can make a ten with two of her numbers then add the third number. What could two of Melonie’s numbers be that would make a ten?

 

Instructional Items

Instructional Item 1 

Using three digits, create an addition sentence that would have a sum of 18. 

 

Instructional Item 2 

The total of three numbers is eleven. What could the three numbers be? 

 

Instructional Item 3 

How many different ways can you get a total of seventeen when you toss three six-sided dice? Record each way. 

 

Instructional Item 4 

Which of the following addition problems will get the same sum as 
a. 2 + 6 + 2 + 4? 
b. 2+4+8 
c. 4+8+2 
d. 8+6 
e. 10+3+1 

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.


Related Courses

Course Number1111 Course Title222
5012030: Grade One Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7712020: Access Mathematics Grade 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012005: Foundational Skills in Mathematics K-2 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.1.AR.1.AP.1 Apply the commutative property of addition to find a sum of two whole numbers within 20.


Related Resources

Formative Assessments

Name Description
Adding Three Whole Numbers

Students are asked to solve word problems that call for addition of three addends.

Tickets to the School Carnival

Students are asked to solve word problems that have three addends.

Lemons and Oranges

Students are given pairs of word problems that can be solved using the Commutative (and/or Associative) Property of addition.

Bean Bag Toss

Students are asked to solve word problems that call for addition of three addends.

Canned Food Drive

Students are asked to solve word problems that call for addition of three addends.

Lesson Plans

Name Description
Fairycat Bookstore

In this Model Eliciting Activity, MEA, students will work in small groups to determine a procedure for deciding which book series they would like in their classroom library. Students will use information presented in pictographs and tally charts to determine this ranking. Then, in the twist, students will have to consider the cost of the series and what they will learn from each.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

Fill It Up - Piñatas!

This MEA focuses on students' problem solving skills. After reading a story about what is in a piñata, students are asked to help a company find the best way to fill a piñata. It focuses on math skills, including counting and adding three numbers to make 20.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.

Show It Another Way

In this lesson, students will apply properties of addition in order to add three whole numbers. Students will then decompose the sum using tens and ones.

Three's a Charm: 3-Number Addition

In this lesson, students will use properties of operations to solve word problems that will require them to add 3 whole numbers whose sum is less than or equal to 20.

Pizza Party Planners

In the story Curious George and the Pizza Party (by Rey, H.A., and Margret Rey), Curious George attends a pizza party for a friend. Now the man with the yellow hat wants to plan his own pizza party for Curious George, but he needs the students' help. Help the man with the yellow hat use the data about the different pizza companies in his area to rank the options from best to worst, considering the toppings offered, crust options, prices, and customer satisfaction ratings. Then the students will use the special promotions from each pizza company and their math skills to figure out which pizza place offers the best deals. Each team of students will write letters to the man with the yellow hat explaining how they ranked the companies and why they chose their rankings to help him choose the best pizza for George's party.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.

Make a Ten To Make Adding Easy!

In this lesson students will add two-digit numbers to one-digit numbers by using the "make a ten" strategy. Students will decompose a two-digit number using expanded form, make a ten, and then add. This lesson is an important lesson for students to be able to add greater numbers as they get into higher grade levels.

Coin Combinations: How else can you pay for that?

In this lesson, students will learn that there can be multiple ways (multiple coin combinations) to reach a given money amount. Using money manipulatives, students will work cooperatively and independently to practice finding different coin combinations for a given money amount. Students will also become comfortable knowing that there are multiple ways to reach a correct answer.

Mission: Addition – Adding 3 Numbers

This activity introduces and provides practice for adding three whole numbers and includes three center activities for independent practice.

Perspectives Video: Teaching Idea

Name Description
Connecting Geometry to Numbers

Unlock an effective teaching strategy for connecting geometry and numbers in order to build number sense in this Teacher Perspectives video for educators.

Problem-Solving Task

Name Description
$20 Dot Map

The language for this task is written above a 1st grade reading level, so it will need to be introduced verbally by the teacher. This problem helps students to practice adding three numbers whose sum are 20 or less. It is an open-ended problem with many solutions.

Tutorial

Name Description
Adding 5 + 3 + 6

Learn how to add 5 + 3 + 6.

Student Resources

Tutorial

Name Description
Adding 5 + 3 + 6:

Learn how to add 5 + 3 + 6.



Parent Resources

Problem-Solving Task

Name Description
$20 Dot Map:

The language for this task is written above a 1st grade reading level, so it will need to be introduced verbally by the teacher. This problem helps students to practice adding three numbers whose sum are 20 or less. It is an open-ended problem with many solutions.



Printed On:4/16/2025 10:42:30 AM
Print Page | Close this window