|
Generated on 9/15/2025 at 10:53 AM |
The webpage this document was printed/exported from can be found at the following URL:
https://www.cpalms.org/PreviewIdea/Preview/1507
https://www.cpalms.org/PreviewIdea/Preview/1507
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Standard 1 : Extend the properties of exponents to rational exponents. (Algebra 1 - Major Cluster) (Algebra 2 - Major Cluster)Archived
Cluster Standards
This cluster includes the following benchmarks.
Visit the specific benchmark webpage to find related instructional resources.
- MAFS.912.N-RN.1.1 : Explain how the definition of the meaning of rational exponents
follows from extending the properties of integer exponents to
those values, allowing for a notation for radicals in terms of rational
exponents. For example, we define
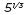to be the cube root of 5
because we want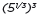 
= 
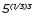to hold, so must equal 5. - MAFS.912.N-RN.1.2 : Rewrite expressions involving radicals and rational exponents using the properties of exponents.
Cluster Information
Number:
MAFS.912.N-RN.1
Title:
Extend the properties of exponents to rational exponents. (Algebra 1 - Major Cluster) (Algebra 2 - Major Cluster)
Type:
Cluster
Subject:
Mathematics - Archived
Grade:
912
Domain-Subdomain
Number & Quantity: The Real Number System
Cluster Access Points
This cluster includes the following Access Points.
- MAFS.912.N-RN.1.AP.2a : Convert from radical representation to using rational exponents and vice versa.
- MAFS.912.N-RN.1.AP.1a : Understand that the denominator of the rational exponent is the root index and the numerator is the exponent of the radicand (e.g., 51/2 = √5). Extend the properties of exponents to justify that (51/2)2=5
- MAFS.912.N-RN.1.AP.1b : Extend the properties of exponents to justify that (51/2)2=5
Cluster Resources
Vetted resources educators can use to teach the concepts and skills in this topic.
Original Student Tutorials
- Solving Rational Equations: Cross Multiplying: Learn how to solve rational linear and quadratic equations using cross multiplication in this interactive tutorial.
- The Radical Puzzle: Learn to rewrite products involving radicals and rational exponents using properties of exponents in this interactive tutorial.
Formative Assessments
- Roots and Exponents: Students are asked to rewrite the square root of five in exponential form and justify their choice of exponent.
- Rational Exponents and Roots: Students asked to show that two forms of an expression (exponential and radical) are equivalent.
- Rational Exponents - 4: Students are asked to rewrite expressions involving radicals and rational exponents in equivalent forms.
- Rational Exponents - 2: Students are asked to convert numerical expressions from exponential to radical form.
- Rational Exponents - 3: Students are asked to convert a product of a radical and exponential expression to a single power of two.
- Rational Exponents - 1: Students are asked to convert numerical expressions from radical to exponential form.
Lesson Plans
- Simply Radical!: Students will simplify and perform operations on radical expressions. Pairs of students will work on problems at different complexity levels that lead to the same solution. The students will challenge each other to prove their solutions are correct. This activity does not address rational exponents.
- Manipulating Radicals: This lesson unit is intended to help you assess how well students are able to:
- Use the properties of exponents, including rational exponents, and manipulate algebraic statements involving radicals.
- Discriminate between equations and identities.
There is also an opportunity to consider the role of the imaginary number
, but this is optional.
Problem-Solving Tasks
- Checking a Calculation of a Decimal Exponent: In this example, students use properties of rational exponents and other algebraic concepts to compare and verify the relative size of two real numbers that involve decimal exponents.
- Extending the Definitions of Exponents, Variation 2: The goal of this task is to develop an understanding of rational exponents (MAFS.912.N-RN.1.1); however, it also raises important issues about distinguishing between linear and exponential behavior (MAFS.912.F-LE.1.1c) and it requires students to create an equation to model a context (MAFS.912.A-CED.1.2).
- Rational or Irrational?: This makes for a good follow-up task on rational irrational numbers after the students have been acquainted with some of the more basic properties, asking students to reason about rational and irrational numbers (N-RN.3) in a variety of ways. In addition to eliciting several different types of reasoning, the task requires students to rewrite radical expressions in which the radicand is divisible by a a perfect square.
Tutorial
- Power of a Power Property: This tutorial demonstrates how to use the power of a power property with both numerals and variables.
Unit/Lesson Sequence
- Sample Algebra 1 Curriculum Plan Using CMAP: This sample Algebra 1 CMAP is a fully customizable resource and curriculum-planning tool that provides a framework for the Algebra 1 Course. The units and standards are customizable and the CMAP allows instructors to add lessons, worksheets, and other resources as needed. This CMAP also includes rows that automatically filter and display Math Formative Assessments System tasks, E-Learning Original Student Tutorials and Perspectives Videos that are aligned to the standards, available on CPALMS.
Learn more about the sample Algebra 1 CMAP, its features and customizability by watching the following video:
Using this CMAP
To view an introduction on the CMAP tool, please .
To view the CMAP, click on the "Open Resource Page" button above; be sure you are logged in to your iCPALMS account.
To use this CMAP, click on the "Clone" button once the CMAP opens in the "Open Resource Page." Once the CMAP is cloned, you will be able to see it as a class inside your iCPALMS My Planner (CMAPs) app.
To access your My Planner App and the cloned CMAP, click on the iCPALMS tab in the top menu.
All CMAP tutorials can be found within the iCPALMS Planner App or at the following URL: http://www.cpalms.org/support/tutorials_and_informational_videos.aspx
Video/Audio/Animations
- Roots and Unit Fraction Exponents: Exponents are not only integers. They can also be fractions. Using the rules of exponents, we can see why a number raised to the power " one over n" is equivalent to the nth root of that number.
- Rational Exponents: Exponents are not only integers and unit fractions. An exponent can be any rational number expressed as the quotient of two integers.
- Simplifying Radical Expressions: Radical expressions can often be simplified by moving factors which are perfect roots out from under the radical sign.