Standard 4 : Integral Calculus (Archived)



This document was generated on CPALMS - www.cpalms.org

Understand that integration is used to find areas, and evaluate integrals using rectangular approximations. From this, develop the idea that integration is the inverse operation to differentiation — the Fundamental Theorem of Calculus. Use this result to find definite and indefinite integrals, including using the method of integration by substitution. Apply approximate methods, such as the Trapezoidal Rule, to find definite integrals. Define integrals using Riemann sums, use the Fundamental Theorem of Calculus to find integrals using antiderivatives, and use basic properties of integrals. Integrate by substitution, and find approximate integrals.

General Information

Number: MAFS.912.C.4
Title: Integral Calculus
Type: Cluster
Subject: Mathematics - Archived
Grade: 912
Domain-Subdomain: Calculus

Related Standards

This cluster includes the following benchmarks
Code Description
MAFS.912.C.4.1: Use rectangle approximations to find approximate values of integrals.
MAFS.912.C.4.2: Calculate the values of Riemann Sums over equal subdivisions using left, right, and midpoint evaluation points.
MAFS.912.C.4.3: Interpret a definite integral as a limit of Riemann sums.
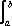MAFS.912.C.4.4: Interpret a definite integral of the rate of change of a quantity over an interval as the change of the quantity over the interval. That is, integral a of b f'(x)dx = f(b) - f(a) (fundamental theorem of calculus).
MAFS.912.C.4.5: Use the Fundamental Theorem of Calculus to evaluate definite and indefinite integrals and to represent particular antiderivatives. Perform analytical and graphical analysis of functions so defined.
MAFS.912.C.4.6: Use these properties of definite integrals:
  • [f(x) + g(x)]dx =  f(x)dx + g(x)dx
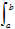  • k • f(x)dx = k f(x)dx
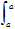  •  f(x)dx = 0
  •  f(x)dx = - f(x)dx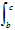
  •  f(x)dx + f(x)dx = f(x)dx
  • If f(x) ≤ g(x) on [a, b], then f(x)dx ≤ g(x)dx
MAFS.912.C.4.7: Use integration by substitution (or change of variable) to find values of integrals.
MAFS.912.C.4.8: Use Riemann Sums, the Trapezoidal Rule, and technology to approximate definite integrals of functions represented algebraically, geometrically, and by tables of values.