| Name |
Description |
| MA.912.AR.2.5: | Solve and graph mathematical and real-world problems that are modeled with linear functions. Interpret key features and determine constraints in terms of the context.Clarifications:
Clarification 1: Key features are limited to domain, range, intercepts and rate of change.Clarification 2: Instruction includes the use of standard form, slope-intercept form and point-slope form. Clarification 3: Instruction includes representing the domain, range and constraints with inequality notation, interval notation or set-builder notation. Clarification 4: Within the Algebra 1 course, notations for domain, range and constraints are limited to inequality and set-builder. Clarification 5: Within the Mathematics for Data and Financial Literacy course, problem types focus on money and business.
|
Examples:
Algebra 1 Example: Lizzy’s mother uses the function C(p)=450+7.75p, where C(p) represents the total cost of a rental space and p is the number of people attending, to help budget Lizzy’s 16th birthday party. Lizzy’s mom wants to spend no more than $850 for the party. Graph the function in terms of the context. |
|
| MA.912.AR.5.3: | Given a mathematical or real-world context, classify an exponential function as representing growth or decay.Clarifications:
Clarification 1: Within the Algebra 1 course, exponential functions are limited to the forms 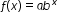 , where b is a whole number greater than 1 or a unit fraction, or , where b is a whole number greater than 1 or a unit fraction, or 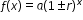 , where , where 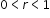 . .
|
|
| MA.912.AR.5.4: | Write an exponential function to represent a relationship between two quantities from a graph, a written description or a table of values within a mathematical or real-world context. |
| MA.912.AR.5.5: | Given an expression or equation representing an exponential function, reveal the constant percent rate of change per unit interval using the properties of exponents. Interpret the constant percent rate of change in terms of a real-world context. |
| MA.912.AR.5.6: | Given a table, equation or written description of an exponential function, graph that function and determine its key features.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; constant percent rate of change; end behavior and asymptotes.
Clarification 2: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation.
Clarification 3: Within the Algebra 1 course, notations for domain and range are limited to inequality and set-builder.
Clarification 4: Within the Algebra 1 course, exponential functions are limited to the forms
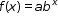 , where b is a whole number greater than 1 or a unit fraction or , where b is a whole number greater than 1 or a unit fraction or 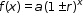 , where , where 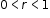 . . |
|
| MA.912.DP.1.1: | Given a set of data, select an appropriate method to represent the data, depending on whether it is numerical or categorical data and on whether it is univariate or bivariate.Clarifications:
Clarification 1: Instruction includes discussions regarding the strengths and weaknesses of each data display.
Clarification 2: Numerical univariate includes histograms, stem-and-leaf plots, box plots and line plots; numerical bivariate includes scatter plots and line graphs; categorical univariate includes bar charts, circle graphs, line plots, frequency tables and relative frequency tables; and categorical bivariate includes segmented bar charts, joint frequency tables and joint relative frequency tables.
Clarification 3: Instruction includes the use of appropriate units and labels and, where appropriate, using technology to create data displays.
|
|
| MA.912.DP.1.2: | Interpret data distributions represented in various ways. State whether the data is numerical or categorical, whether it is univariate or bivariate and interpret the different components and quantities in the display.Clarifications:
Clarification 1: Within the Probability and Statistics course, instruction includes the use of spreadsheets and technology. |
|
| MA.912.DP.2.1: | For two or more sets of numerical univariate data, calculate and compare the appropriate measures of center and measures of variability, accounting for possible effects of outliers. Interpret any notable features of the shape of the data distribution.Clarifications:
Clarification 1: The measure of center is limited to mean and median. The measure of variation is limited to range, interquartile range, and standard deviation.Clarification 2: Shape features include symmetry or skewness and clustering. Clarification 3: Within the Probability and Statistics course, instruction includes the use of spreadsheets and technology.
|
|
| MA.912.DP.2.4: | Fit a linear function to bivariate numerical data that suggests a linear association and interpret the slope and y-intercept of the model. Use the model to solve real-world problems in terms of the context of the data.Clarifications:
Clarification 1: Instruction includes fitting a linear function both informally and formally with the use of technology.Clarification 2: Problems include making a prediction or extrapolation, inside and outside the range of the data, based on the equation of the line of fit.
|
|
| MA.912.DP.2.9: | Fit an exponential function to bivariate numerical data that suggests an exponential association. Use the model to solve real-world problems in terms of the context of the data.Clarifications:
Clarification 1: Instruction focuses on determining whether an exponential model is appropriate by taking the logarithm of the dependent variable using spreadsheets and other technology.Clarification 2: Instruction includes determining whether the transformed scatterplot has an appropriate line of best fit, and interpreting the y-intercept and slope of the line of best fit. Clarification 3: Problems include making a prediction or extrapolation, inside and outside the range of the data, based on the equation of the line of fit.
|
|
| MA.912.DP.4.1: | Describe events as subsets of a sample space using characteristics, or categories, of the outcomes, or as unions, intersections or complements of other events. |
| MA.912.DP.4.2: | Determine if events A and B are independent by calculating the product of their probabilities. |
| MA.912.DP.4.3: | Calculate the conditional probability of two events and interpret the result in terms of its context. |
| MA.912.DP.4.4: | Interpret the independence of two events using conditional probability. |
| MA.912.DP.4.5: | Given a two-way table containing data from a population, interpret the joint and marginal relative frequencies as empirical probabilities and the conditional relative frequencies as empirical conditional probabilities. Use those probabilities to determine whether characteristics in the population are approximately independent.Clarifications:
Clarification 1: Instruction includes the connection between mathematical probability and applied statistics. |
Examples:
Example: A company has a commercial for their new grill. A population of people are surveyed to determine whether or not they have seen the commercial and whether or not they have purchased the product. Using this data, calculate the empirical conditional probabilities that a person who has seen the commercial did or did not purchase the grill. |
|
| MA.912.DP.4.6: | Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. |
| MA.912.DP.4.7: | Apply the addition rule for probability, taking into consideration whether the events are mutually exclusive, and interpret the result in terms of the model and its context. |
| MA.912.DP.4.8: | Apply the general multiplication rule for probability, taking into consideration whether the events are independent, and interpret the result in terms of the context. |
| MA.912.DP.4.9: | Apply the addition and multiplication rules for counting to solve mathematical and real-world problems, including problems involving probability. |
| MA.912.DP.4.10: | Given a mathematical or real-world situation, calculate the appropriate permutation or combination. |
| MA.912.F.1.6: | Compare key features of linear and nonlinear functions each represented algebraically, graphically, in tables or written descriptions.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; end behavior and asymptotes. Clarification 2: Within the Algebra 1 course, functions other than linear, quadratic or exponential must be represented graphically. Clarification 3: Within the Algebra 1 course, instruction includes verifying that a quantity increasing exponentially eventually exceeds a quantity increasing linearly or quadratically.
|
|
| MA.912.F.1.8: | Determine whether a linear, quadratic or exponential function best models a given real-world situation.Clarifications:
Clarification 1: Instruction includes recognizing that linear functions model situations in which a quantity changes by a constant amount per unit interval; that quadratic functions model situations in which a quantity increases to a maximum, then begins to decrease or a quantity decreases to a minimum, then begins to increase; and that exponential functions model situations in which a quantity grows or decays by a constant percent per unit interval. Clarification 2: Within this benchmark, the expectation is to identify the type of function from a written description or table.
|
|
| MA.912.FL.3.1: | Compare simple, compound and continuously compounded interest over time.Clarifications:
Clarification 1: Instruction includes taking into consideration the annual percentage rate (APR) when comparing simple and compound interest. |
|
| MA.912.FL.3.2: | Solve real-world problems involving simple, compound and continuously compounded interest.Clarifications:
Clarification 1: Within the Algebra 1 course, interest is limited to simple and compound. |
Examples:
Example: Find the amount of money on deposit at the end of 5 years if you started with $500 and it was compounded quarterly at 6% interest per year. Example: Joe won $25,000 on a lottery scratch-off ticket. How many years will it take at 6% interest compounded yearly for his money to double?
|
|
| MA.912.FL.3.4: | Explain the relationship between simple interest and linear growth. Explain the relationship between compound interest and exponential growth and the relationship between continuously compounded interest and exponential growth.Clarifications:
Clarification 1: Within the Algebra 1 course, exponential growth is limited to compound interest. |
|
| MA.912.GR.1.6: | Solve mathematical and real-world problems involving congruence or similarity in two-dimensional figures.Clarifications:
Clarification 1: Instruction includes demonstrating that two-dimensional figures are congruent or similar based on given information. |
|
| MA.912.GR.2.4: | Determine symmetries of reflection, symmetries of rotation and symmetries of translation of a geometric figure.Clarifications:
Clarification 1: Instruction includes determining the order of each symmetry.Clarification 2: Instruction includes the connection between tessellations of the plane and symmetries of translations.
|
|
| MA.912.GR.4.3: | Extend previous understanding of scale drawings and scale factors to determine how dilations affect the area of two-dimensional figures and the surface area or volume of three-dimensional figures.
Examples:
Example: Mike is having a graduation party and wants to make sure he has enough pizza. Which option would provide more pizza for his guests: one 12-inch pizza or three 6-inch pizzas? |
|
| MA.912.GR.4.4: | Solve mathematical and real-world problems involving the area of two-dimensional figures.Clarifications:
Clarification 1: Instruction includes concepts of population density based on area. |
Examples:
Example: A town has 23 city blocks, each of which has dimensions of 1 quarter mile by 1 quarter mile, and there are 4500 people in the town. What is the population density of the town? |
|
| MA.912.GR.4.5: | Solve mathematical and real-world problems involving the volume of three-dimensional figures limited to cylinders, pyramids, prisms, cones and spheres.Clarifications:
Clarification 1: Instruction includes concepts of density based on volume.
Clarification 2: Instruction includes using Cavalieri’s Principle to give informal arguments about the formulas for the volumes of right and non-right cylinders, pyramids, prisms and cones.
|
Examples:
Example: A cylindrical swimming pool is filled with water and has a diameter of 10 feet and height of 4 feet. If water weighs 62.4 pounds per cubic foot, what is the total weight of the water in a full tank to the nearest pound? |
|
| MA.912.GR.4.6: | Solve mathematical and real-world problems involving the surface area of three-dimensional figures limited to cylinders, pyramids, prisms, cones and spheres. |
| MA.912.LT.4.1: | Translate propositional statements into logical arguments using propositional variables and logical connectives. |
| MA.912.LT.4.2: | Determine truth values of simple and compound statements using truth tables. |
| MA.912.LT.4.3: | Identify and accurately interpret “if…then,” “if and only if,” “all” and “not” statements. Find the converse, inverse and contrapositive of a statement.Clarifications:
Clarification 1: Instruction focuses on recognizing the relationships between an “if…then” statement and the converse, inverse and contrapositive of that statement.
Clarification 2: Within the Geometry course, instruction focuses on the connection to proofs within the course.
|
|
| MA.912.LT.4.4: | Represent logic operations, such as AND, OR, NOT, NOR, and XOR, using logical symbolism to solve problems. |
| MA.912.LT.4.5: | Determine whether two propositions are logically equivalent. |
| MA.912.LT.4.9: | Construct logical arguments using laws of detachment, syllogism, tautology, contradiction and Euler Diagrams. |
| MA.912.LT.4.10: | Judge the validity of arguments and give counterexamples to disprove statements.Clarifications:
Clarification 1: Within the Geometry course, instruction focuses on the connection to proofs within the course. |
|
| MA.912.LT.5.1: | Given two sets, determine whether the two sets are equivalent and whether one set is a subset of another. Given one set, determine its power set. |
| MA.912.LT.5.4: | Perform the set operations of taking the complement of a set and the union, intersection, difference and product of two sets.Clarifications:
Clarification 1: Instruction includes the connection to probability and the words AND, OR and NOT. |
|
| MA.912.LT.5.5: | Explore relationships and patterns and make arguments about relationships between sets using Venn Diagrams. |
| MA.912.LT.5.6: | Prove set relations, including DeMorgan’s Laws and equivalence relations. |
| MA.912.T.1.2: | Solve mathematical and real-world problems involving right triangles using trigonometric ratios and the Pythagorean Theorem.Clarifications:
Clarification 1: Instruction includes procedural fluency with the relationships of side lengths in special right triangles having angle measures of 30°-60°-90° and 45°-45°-90°. |
|
| MA.K12.MTR.1.1: | Actively participate in effortful learning both individually and collectively. Mathematicians who participate in effortful learning both individually and with others:
- Analyze the problem in a way that makes sense given the task.
- Ask questions that will help with solving the task.
- Build perseverance by modifying methods as needed while solving a challenging task.
- Stay engaged and maintain a positive mindset when working to solve tasks.
- Help and support each other when attempting a new method or approach.
Clarifications:
Teachers who encourage students to participate actively in effortful learning both individually and with others:
- Cultivate a community of growth mindset learners.
- Foster perseverance in students by choosing tasks that are challenging.
- Develop students’ ability to analyze and problem solve.
- Recognize students’ effort when solving challenging problems.
|
|
| MA.K12.MTR.2.1: | Demonstrate understanding by representing problems in multiple ways. Mathematicians who demonstrate understanding by representing problems in multiple ways: - Build understanding through modeling and using manipulatives.
- Represent solutions to problems in multiple ways using objects, drawings, tables, graphs and equations.
- Progress from modeling problems with objects and drawings to using algorithms and equations.
- Express connections between concepts and representations.
- Choose a representation based on the given context or purpose.
Clarifications:
Teachers who encourage students to demonstrate understanding by representing problems in multiple ways: - Help students make connections between concepts and representations.
- Provide opportunities for students to use manipulatives when investigating concepts.
- Guide students from concrete to pictorial to abstract representations as understanding progresses.
- Show students that various representations can have different purposes and can be useful in different situations.
|
|
| MA.K12.MTR.3.1: | Complete tasks with mathematical fluency. Mathematicians who complete tasks with mathematical fluency: - Select efficient and appropriate methods for solving problems within the given context.
- Maintain flexibility and accuracy while performing procedures and mental calculations.
- Complete tasks accurately and with confidence.
- Adapt procedures to apply them to a new context.
- Use feedback to improve efficiency when performing calculations.
Clarifications:
Teachers who encourage students to complete tasks with mathematical fluency:- Provide students with the flexibility to solve problems by selecting a procedure that allows them to solve efficiently and accurately.
- Offer multiple opportunities for students to practice efficient and generalizable methods.
- Provide opportunities for students to reflect on the method they used and determine if a more efficient method could have been used.
|
|
| MA.K12.MTR.4.1: | Engage in discussions that reflect on the mathematical thinking of self and others. Mathematicians who engage in discussions that reflect on the mathematical thinking of self and others: - Communicate mathematical ideas, vocabulary and methods effectively.
- Analyze the mathematical thinking of others.
- Compare the efficiency of a method to those expressed by others.
- Recognize errors and suggest how to correctly solve the task.
- Justify results by explaining methods and processes.
- Construct possible arguments based on evidence.
Clarifications:
Teachers who encourage students to engage in discussions that reflect on the mathematical thinking of self and others:- Establish a culture in which students ask questions of the teacher and their peers, and error is an opportunity for learning.
- Create opportunities for students to discuss their thinking with peers.
- Select, sequence and present student work to advance and deepen understanding of correct and increasingly efficient methods.
- Develop students’ ability to justify methods and compare their responses to the responses of their peers.
|
|
| MA.K12.MTR.5.1: | Use patterns and structure to help understand and connect mathematical concepts. Mathematicians who use patterns and structure to help understand and connect mathematical concepts: - Focus on relevant details within a problem.
- Create plans and procedures to logically order events, steps or ideas to solve problems.
- Decompose a complex problem into manageable parts.
- Relate previously learned concepts to new concepts.
- Look for similarities among problems.
- Connect solutions of problems to more complicated large-scale situations.
Clarifications:
Teachers who encourage students to use patterns and structure to help understand and connect mathematical concepts:- Help students recognize the patterns in the world around them and connect these patterns to mathematical concepts.
- Support students to develop generalizations based on the similarities found among problems.
- Provide opportunities for students to create plans and procedures to solve problems.
- Develop students’ ability to construct relationships between their current understanding and more sophisticated ways of thinking.
|
|
| MA.K12.MTR.6.1: | Assess the reasonableness of solutions. Mathematicians who assess the reasonableness of solutions: - Estimate to discover possible solutions.
- Use benchmark quantities to determine if a solution makes sense.
- Check calculations when solving problems.
- Verify possible solutions by explaining the methods used.
- Evaluate results based on the given context.
Clarifications:
Teachers who encourage students to assess the reasonableness of solutions:- Have students estimate or predict solutions prior to solving.
- Prompt students to continually ask, “Does this solution make sense? How do you know?”
- Reinforce that students check their work as they progress within and after a task.
- Strengthen students’ ability to verify solutions through justifications.
|
|
| MA.K12.MTR.7.1: | Apply mathematics to real-world contexts. Mathematicians who apply mathematics to real-world contexts: - Connect mathematical concepts to everyday experiences.
- Use models and methods to understand, represent and solve problems.
- Perform investigations to gather data or determine if a method is appropriate.
• Redesign models and methods to improve accuracy or efficiency.
Clarifications:
Teachers who encourage students to apply mathematics to real-world contexts:- Provide opportunities for students to create models, both concrete and abstract, and perform investigations.
- Challenge students to question the accuracy of their models and methods.
- Support students as they validate conclusions by comparing them to the given situation.
- Indicate how various concepts can be applied to other disciplines.
|
|
| ELA.K12.EE.1.1: | Cite evidence to explain and justify reasoning.Clarifications:
K-1 Students include textual evidence in their oral communication with guidance and support from adults. The evidence can consist of details from the text without naming the text. During 1st grade, students learn how to incorporate the evidence in their writing.2-3 Students include relevant textual evidence in their written and oral communication. Students should name the text when they refer to it. In 3rd grade, students should use a combination of direct and indirect citations. 4-5 Students continue with previous skills and reference comments made by speakers and peers. Students cite texts that they’ve directly quoted, paraphrased, or used for information. When writing, students will use the form of citation dictated by the instructor or the style guide referenced by the instructor. 6-8 Students continue with previous skills and use a style guide to create a proper citation. 9-12 Students continue with previous skills and should be aware of existing style guides and the ways in which they differ.
|
|
| ELA.K12.EE.2.1: | Read and comprehend grade-level complex texts proficiently.Clarifications:
See Text Complexity for grade-level complexity bands and a text complexity rubric. |
|
| ELA.K12.EE.3.1: | Make inferences to support comprehension.Clarifications:
Students will make inferences before the words infer or inference are introduced. Kindergarten students will answer questions like “Why is the girl smiling?” or make predictions about what will happen based on the title page.
Students will use the terms and apply them in 2nd grade and beyond. |
|
| ELA.K12.EE.4.1: | Use appropriate collaborative techniques and active listening skills when engaging in discussions in a variety of situations.Clarifications:
In kindergarten, students learn to listen to one another respectfully.In grades 1-2, students build upon these skills by justifying what they are thinking. For example: “I think ________ because _______.” The collaborative conversations are becoming academic conversations. In grades 3-12, students engage in academic conversations discussing claims and justifying their reasoning, refining and applying skills. Students build on ideas, propel the conversation, and support claims and counterclaims with evidence.
|
|
| ELA.K12.EE.5.1: | Use the accepted rules governing a specific format to create quality work.Clarifications:
Students will incorporate skills learned into work products to produce quality work. For students to incorporate these skills appropriately, they must receive instruction. A 3rd grade student creating a poster board display must have instruction in how to effectively present information to do quality work. |
|
| ELA.K12.EE.6.1: | Use appropriate voice and tone when speaking or writing.Clarifications:
In kindergarten and 1st grade, students learn the difference between formal and informal language. For example, the way we talk to our friends differs from the way we speak to adults. In 2nd grade and beyond, students practice appropriate social and academic language to discuss texts. |
|
| ELD.K12.ELL.MA.1: | English language learners communicate information, ideas and concepts necessary for academic success in the content area of Mathematics. |

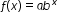 , where b is a whole number greater than 1 or a unit fraction, or
, where b is a whole number greater than 1 or a unit fraction, or 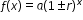 , where
, where 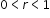 .
.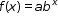 , where b is a whole number greater than 1 or a unit fraction or
, where b is a whole number greater than 1 or a unit fraction or 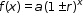 , where
, where 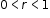 .
.