Clarifications:
Essential Understandings
Concrete:
- Use tools to manipulate the frequency of a sine or cosine graph (e.g., calculator, graphing software, coordinate grid).
- Understand the following concepts and vocabulary: radian, degree, frequency, period, amplitude, maximum, minimum, function, cycle, interval, convert, sine, cosine, ordered pair, trigonometric functions.
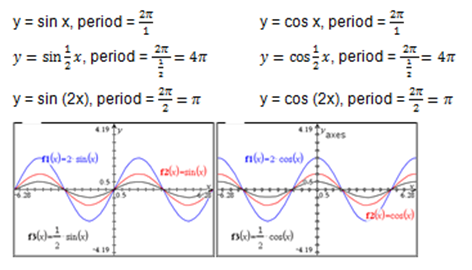
- Understand that a sine function can be written as y=Asin(Bx) where A= amplitude, B= change in period.
- Understand that a cosine function can be written as y=Acos(Bx) where A= amplitude, B= change in period.
- Understand that a periodic function is a wave-like function that repeats a pattern of y-values at regular intervals. One complete repetition of the pattern is called a cycle. The period of a function is the horizontal length of one complete cycle.
- Understand that a basic sine or cosine function has a period (frequency) of
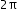. - Understand that B is the number of cycles you see in a 0 to
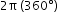interval. For example: y=sin(1/2 x), B = 1/2 therefore the function will only have half a cycle from 0 to 2π. The full cycle will be completed in 
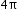instead of 
.
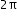| Number: MAFS.912.F-TF.2.AP.5d | Category: Access Points |
| Date Adopted or Revised: 06/14 |
Cluster:
Model periodic phenomena with trigonometric functions. (Algebra 2 - Additional Cluster) : Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters. |