Access Point #: MAFS.912.N-CN.3.AP.7a (Archived Access Point)


This document was generated on CPALMS - www.cpalms.org



Use the quadratic formula 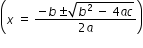begin mathsize 12px style open parentheses x space equals space fraction numerator negative b plus-or-minus square root of b to the power of 2 space end exponent minus space 4 a c end root over denominator 2 a end fraction close parentheses end style to find solutions to quadratic equations that have complex solutions. 

Clarifications:

Essential Understandings

Concrete:

  • Use a tool to determine whether the quadratic function crosses the x-axis. Click Here 
  • Use a graphing tool or graphing software to find the roots (where the function intersects the x-axis) of a function.
  • Label a, b, and c values in the quadratic function.
  • begin mathsize 12px style a x squared space plus space b x space plus space c space equals space 0 end style
Representation:
  • Understand the following concepts and vocabulary: root, discriminant, factor, quadratic, integer, imaginary number, real number, complex number, quadratic equation, quadratic formula, square root, solution, terms, coefficient, complex solution, intercept, intersect.
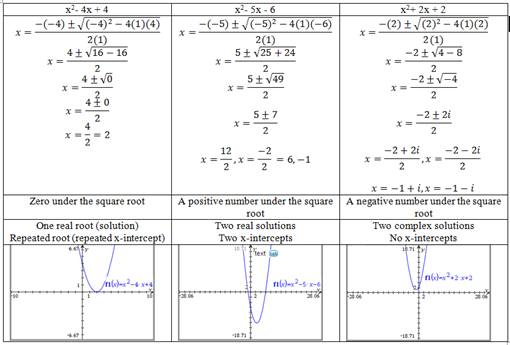
  • Understand that a root is the point where a function intersects the x-axis.
  • Substitute values into the quadratic function.
  • Understand that a quadratic function that intersects the x-axis has real roots. A quadratic function that does not intersect the x-axis has imaginary roots.

    Image of 3 different formula scenarios and 3 different graph scenarios.
  • Substitute values into the quadratic formula.
  • Use the quadratic formula to find the roots of a function.

Number: MAFS.912.N-CN.3.AP.7a Category: Access Points
Date Adopted or Revised: 06/14 Cluster: Use complex numbers in polynomial identities and equations. (Algebra 2 - Additional Cluster) : 

Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.