Access Point #: MAFS.912.G-SRT.1.AP.1b (Archived Access Point)


This document was generated on CPALMS - www.cpalms.org



Given a center and a scale factor, verify experimentally that when performing dilations of a line segment, the pre-image, the segment which becomes the image is longer or shorter based on the ratio given by the scale factor.

Clarifications:

Essential Understandings

Concrete:

  • Using manipulatives (i.e., patty paper, snap cubes) demonstrate how the line segment pre-image could increase or decrease by the scale factor, for example, a line segment that is 2 snap cubes long could increase by a scale factor of two by putting it next to a line segment that has four snap cubes.
  • Online activity manipulating line segments with a scale factor. Click Here
Representation:
  • A dilation is a transformation (notation DK) that produces an image that is the same shape as the original, but is a different size. A dilation stretches or shrinks the original figure.
  • The description of a dilation includes the scale factor (or ratio) and the center of the dilation. The center of dilation is a fixed point in the plane about which all points are expanded or contracted. It is the only invariant point under a dilation.

    Image of a triangle labeled with points to show dilation.
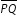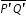  • The pre-image begin mathsize 12px style stack P Q with bar on top end style is three times bigger than the image begin mathsize 12px style stack P apostrophe Q apostrophe with bar on top end style.

Number: MAFS.912.G-SRT.1.AP.1b Category: Access Points
Date Adopted or Revised: 07/14 Cluster: Understand similarity in terms of similarity transformations. (Geometry - Major Cluster) : 

Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.

Related Standards

Name Description
MAFS.912.G-SRT.1.1: Verify experimentally the properties of dilations given by a center and a scale factor:
  1. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged.
  2. The dilation of a line segment is longer or shorter in the ratio given by the scale factor.



Related Courses

Name Description
1200400: Foundational Skills in Mathematics 9-12
1206300: Informal Geometry
1206310: Geometry
1206320: Geometry Honors
1206330: Analytic Geometry
7912060: Access Informal Geometry
1206315: Geometry for Credit Recovery
7912065: Access Geometry