Clarifications:
Essential Understandings
Concrete:
- Using manipulatives, demonstrate the following transformations:
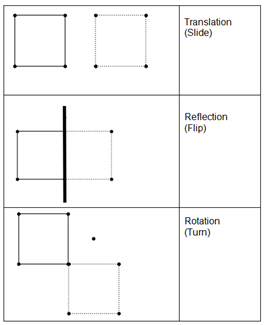
- Teacher resource: Click Here
- A rigid transformation is one in which the pre-image and the image both have the exact same size and shape.
- If one shape can become another using turns, flips and/or slides, then the shapes are congruent. Congruent is two objects with the same shape and same size.
| Number: MAFS.912.G-CO.2.AP.6b | Category: Access Points |
| Date Adopted or Revised: 07/14 |
Cluster:
Understand congruence in terms of rigid motions. (Geometry - Major Cluster) : Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters. |
