
This is a resource from CPALMS (www.cpalms.org) where all educators go for bright ideas!
Resource ID#: 70526
Primary Type: Formative Assessment
Sum of Rational Numbers
Students are asked to define a rational number and then explain why the sum of two rational numbers is rational.
General Information
Attachments
mfas_sumofrationalnumbers_worksheet.docxmfas_sumofrationalnumbers_worksheet.pdf
Formative Assessment Task
This task can be implemented individually, with small groups, or with the whole class.
- The teacher asks the student to complete the problems on the Sum of Rational Numbers worksheet.
- The teacher asks follow-up questions, as needed.
TASK RUBRIC
Getting Started | |
| Misconception/Error The student cannot correctly define a rational number. | |
| Examples of Student Work at this Level The student may be able to provide an example of a rational number. However, the student is unable to write a complete and correct definition. The student says: | |
| Questions Eliciting Thinking You said that a rational number can be written as a fraction. Can you be more specific about the numerator and denominator? What type of numbers must they be? Are there any restrictions on the denominator? What happens when you try to write a rational number as a decimal? Can you explain what you mean by “doesn’t go on forever”? Can you explain what you mean by “can be written as a fraction”? Can you provide examples? Can you give me an example of a number that is not rational? | |
| Instructional Implications Remind the student that the integers consist of the set {…-3, -2, -1, 0, 1, 2, 3, …}. Then, review the definition of a rational number as a number that can be written in the form Challenge the student to review his or her initial explanation of a rational number. Ask the student to correct any errors and revise the explanation. Also, ask the student to provide additional examples of rational numbers. | |
Making Progress | |
| Misconception/Error The student is unable to explain why the sum of two rational numbers must be rational. | |
| Examples of Student Work at this Level The student can define and provide examples of rational numbers. However, the student is unable to explain why the sum of two rational numbers must be rational. The student:
| |
| Questions Eliciting Thinking How do you know that the common denominator is an integer? How could you use variables to model rational numbers and then model the sum of the two rational numbers? | |
| Instructional Implications Review the fact that the integers are closed for addition, subtraction, and multiplication. Guide the student to understand that the rational numbers are closed for addition, subtraction, multiplication, and division. Show that the sum of two rational numbers must be rational by reasoning that if
| |
Got It | |
| Misconception/Error The student provides complete and correct responses to all components of the task. | |
| Examples of Student Work at this Level The student explains that rational numbers can be written as a fraction of two integers with a nonzero denominator. As a result, rational numbers written as decimals are repeating or terminating. The student is able to provide a variety of examples of rational numbers (e.g., whole numbers, integers, fractions, repeating and terminating decimals, and radicals that reduce to a rational number). To show that the sum of two rational numbers must be rational, the student provides a proof such as: Suppose p and q are rational numbers. Since p and q are rational, they can be represented as fractions of integers with nonzero denominators, for example, as | |
| Questions Eliciting Thinking To what number system do both the rational numbers and irrational numbers belong? What is an irrational number? Are there any rational numbers that are also irrational? | |
| Instructional Implications Challenge the student to determine whether each of the following statements is always true, sometimes true, or never true:
| |
Accommodations & Recommendations
Special Materials Needed:
- Sum of Rational Numbers worksheet
Source and Access Information
Aligned Standards
Benchmark(s) of focus
| Name | Description |
| MA.8.NSO.1.1: | Extend previous understanding of rational numbers to define irrational numbers within the real number system. Locate an approximate value of a numerical expression involving irrational numbers on a number line. Clarifications: Clarification 1: Instruction includes the use of number line and rational number approximations, and recognizing pi (π) as an irrational number. Clarification 2: Within this benchmark, the expectation is to approximate numerical expressions involving one arithmetic operation and estimating square roots or pi (π). |





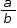 where a and b are integers but
where a and b are integers but 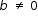 . Use the definition as a way to “build” rational numbers by substituting integers for a and b to form a variety of rational numbers. Then use the definition as a way to show a number (e.g., 0, -8, 12,
. Use the definition as a way to “build” rational numbers by substituting integers for a and b to form a variety of rational numbers. Then use the definition as a way to show a number (e.g., 0, -8, 12, 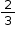 ,
, 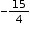 ) is rational by rewriting it as a fraction of integers. Finally, ask the student to convert a variety of rational numbers written in fraction form to decimals and to observe that the decimal representation of a rational number will either terminate or repeat.
) is rational by rewriting it as a fraction of integers. Finally, ask the student to convert a variety of rational numbers written in fraction form to decimals and to observe that the decimal representation of a rational number will either terminate or repeat.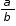 and
and 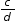 are rational then their sum,
are rational then their sum, 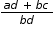 , must be rational since both ac and bd are integers. Ask the student to reason in a similar fashion to show that the rational numbers are closed for subtraction, multiplication, and division.
, must be rational since both ac and bd are integers. Ask the student to reason in a similar fashion to show that the rational numbers are closed for subtraction, multiplication, and division. and
and 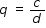 where a, b, c, d, are integers such that
where a, b, c, d, are integers such that 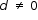 . Then
. Then 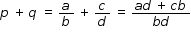 . Since integers are closed under multiplication and addition then ad + cb and bd are also integers. Additionally, since
. Since integers are closed under multiplication and addition then ad + cb and bd are also integers. Additionally, since  . So,
. So, 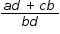 is a fraction of integers with
is a fraction of integers with