Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
-
Also assesses:
- Assessment Limits :
In items where a function is represented by an equation, the function
may be an exponential function with no more than one translation, a
linear function, or a quadratic function.In items where a function is represented by a graph or table, the
function may be any continuous function. - Calculator :
Neutral
- Clarification :
Students will find a solution or an approximate solution for f(x) = g(x)
using a graph.Students will find a solution or an approximate solution for f(x) = g(x)
using a table of values.Students will find a solution or an approximate solution for f(x) = g(x)
using successive approximations that give the solution to a given
place value.Students will justify why the intersection of two functions is a solution
to f(x) = g(x).Students will verify if a set of ordered pairs is a solution of a function.
- Stimulus Attributes :
Items may be set in a mathematical or real-world context.Items may use function notation.
Items must designate the place value accuracy necessary for
approximate solutions. - Response Attributes :
Items may require the student to complete a missing step in an
algebraic justification of the solution of f(x) = g(x).Items may require the student to explain the role of the x-coordinate
and the y-coordinate in the intersection of f(x) = g(x).Items may require the student to explain a process.
Items may require the student to record successive approximations
used to find the solution of f(x) = g(x).
MAFS.912.A-REI.4.10
- Test Item #: Sample Item 1
- Question:
Cora is using successive approximations to estimate a positive solution to f(x)=g(x), where
f(x)=x²+13 and g(x)=3x+14. The table shows her results for different input values of x.
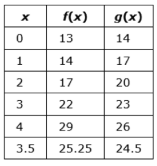
Use Cora's process to find the positive solution, to the nearest tenth, of f(x)=g(x).
- Difficulty: N/A
- Type: EE: Equation Editor
Related Courses
Related Access Points
Related Resources
Formative Assessments
Lesson Plan
Original Student Tutorial
Problem-Solving Tasks
Unit/Lesson Sequence
Virtual Manipulative
MFAS Formative Assessments
Students are asked to find the solution(s) of the equation f(x) = g(x) given the graphs of f and g and explain their reasoning.
Students are asked to explain why the x-coordinate of the intersection of two functions, f and g, is a solution of the equation f(x) = g(x).
Students are asked to find solutions of the equation f(x) = g(x) for two given functions, f and g, by constructing a table of values.
Students are asked to use technology (e.g., spreadsheet, graphing calculator, or dynamic geometry software) to estimate the solutions of the equation f(x) = g(x) for given functions f and g.
Original Student Tutorials Mathematics - Grades 9-12
Follow as we learn why the x-coordinate of the point of intersection of two functions is the solution of the equation f(x) = g(x) in this interactive tutorial.
Student Resources
Original Student Tutorial
Follow as we learn why the x-coordinate of the point of intersection of two functions is the solution of the equation f(x) = g(x) in this interactive tutorial.
Type: Original Student Tutorial
Problem-Solving Tasks
In this task students use verbal descriptions to construct and compare linear and exponential functions and to find where the two functions intersect (F-LE.2, F-LE.3, A-REI.11).
Type: Problem-Solving Task
This classroom task is meant to elicit a variety of different methods of solving a quadratic equation (A-REI.4). Some are straightforward (for example, expanding the square on the right and rearranging the equation so that we can use the quadratic formula); some are simple but clever (reasoning from the fact that x and (2x - 9) have the same square); some use tools (using a graphing calculator to graph the functions f(x) = x^2 and g(x) = (2x-90)^2 and looking for values of x at which the two functions intersect). Some solution methods will work on an arbitrary quadratic equation, while others (such as the last three) may have difficulty or fail if the quadratic equation is not given in a particular form, or if the solutions are not rational numbers.
Type: Problem-Solving Task
Virtual Manipulative
This interactive simulation investigates graphing linear and quadratic equations. Users are given the ability to define and change the coefficients and constants in order to observe resulting changes in the graph(s).
Type: Virtual Manipulative
Parent Resources
Problem-Solving Tasks
In this task students use verbal descriptions to construct and compare linear and exponential functions and to find where the two functions intersect (F-LE.2, F-LE.3, A-REI.11).
Type: Problem-Solving Task
This classroom task is meant to elicit a variety of different methods of solving a quadratic equation (A-REI.4). Some are straightforward (for example, expanding the square on the right and rearranging the equation so that we can use the quadratic formula); some are simple but clever (reasoning from the fact that x and (2x - 9) have the same square); some use tools (using a graphing calculator to graph the functions f(x) = x^2 and g(x) = (2x-90)^2 and looking for values of x at which the two functions intersect). Some solution methods will work on an arbitrary quadratic equation, while others (such as the last three) may have difficulty or fail if the quadratic equation is not given in a particular form, or if the solutions are not rational numbers.
Type: Problem-Solving Task