MAFS.912.N-RN.1.2Archived Standard

loading spinner
Export Print
Rewrite expressions involving radicals and rational exponents using the properties of exponents.
General Information
Subject Area: Mathematics
Grade: 912
Domain-Subdomain: Number & Quantity: The Real Number System
Cluster: Level 1: Recall
Cluster: Extend the properties of exponents to rational exponents. (Algebra 1 - Major Cluster) (Algebra 2 - Major Cluster) -

Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.

Date Adopted or Revised: 02/14
Content Complexity Rating: Level 1: Recall - More Information
Date of Last Rating: 02/14
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications
    Also assesses:
    MAFS.912.N-RN.1.1

    MAFS.912.N-RN.2.3
  • Assessment Limits :
    Expressions should contain no more than three variables.

    For N-RN.1.2, items should not require the student to do more than
    two operations.

  • Calculator :

    Neutral

  • Clarification :
    Students will use the properties of exponents to rewrite a radical
    expression as an expression with a rational exponent.

    Students will use the properties of exponents to rewrite an
    expression with a rational exponent as a radical expression.

    Students will apply the properties of operations of integer exponents
    to expressions with rational exponents.

    Students will apply the properties of operations of integer exponents
    to radical expressions.

    Students will write algebraic proofs that show that a sum or product
    of two rational numbers is rational; that the sum of a rational number
    and an irrational number is irrational; and that the product of a
    nonzero rational number and an irrational number is irrational. 

  • Stimulus Attributes :
    Items should be set in a mathematical context.
  • Response Attributes :
    Items may require the student to complete an algebraic proof.

    Items may require the student to determine equivalent expressions
    or equations.

    Responses with square roots should require the student to rewrite
    the square root so that the radicand has no square factors

Sample Test Items (1)
  • Test Item #: Sample Item 1
  • Question:

    Jeremy determines that 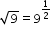begin mathsize 12px style square root of 9 equals 9 to the power of 1 half end exponent end style. Part of his work is shown.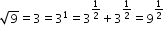

    begin mathsize 12px style square root of 9 equals 3 equals 3 to the power of 1 equals 3 to the power of 1 half end exponent plus 3 to the power of 1 half end exponent equals 9 to the power of 1 half end exponent end style

    Which expression or equation should be placed in the blank to correctly complete Jeremy's work?

  • Difficulty: N/A
  • Type: MC: Multiple Choice

Related Courses

This benchmark is part of these courses.
1200310: Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1200320: Algebra 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1200330: Algebra 2 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1200340: Algebra 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1200370: Algebra 1-A (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1200400: Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1207310: Liberal Arts Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated))
1206330: Analytic Geometry (Specifically in versions: 2014 - 2015 (course terminated))
1200410: Mathematics for College Success (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated))
1200700: Mathematics for College Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated))
7912060: Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated))
7912070: Access Mathematics for Liberal Arts (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 - 2023, 2023 and beyond (current))
7912080: Access Algebra 1A (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))
7912090: Access Algebra 1B (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))
1200315: Algebra 1 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1200335: Algebra 2 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2019 (course terminated))
1200375: Algebra 1-A for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912065: Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current))
7912075: Access Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))
7912095: Access Algebra 2 (Specifically in versions: 2016 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))

Related Access Points

Alternate version of this benchmark for students with significant cognitive disabilities.

Related Resources

Vetted resources educators can use to teach the concepts and skills in this benchmark.

Formative Assessments

Rational Exponents - 4:

Students are asked to rewrite expressions involving radicals and rational exponents in equivalent forms.

Type: Formative Assessment

Rational Exponents - 2:

Students are asked to convert numerical expressions from exponential to radical form.

Type: Formative Assessment

Rational Exponents - 3:

Students are asked to convert a product of a radical and exponential expression to a single power of two.

Type: Formative Assessment

Rational Exponents - 1:

Students are asked to convert numerical expressions from radical to exponential form.

Type: Formative Assessment

Lesson Plans

Simply Radical!:

Students will simplify and perform operations on radical expressions. Pairs of students will work on problems at different complexity levels that lead to the same solution. The students will challenge each other to prove their solutions are correct. This activity does not address rational exponents.

Type: Lesson Plan

Manipulating Radicals:

This lesson unit is intended to help you assess how well students are able to:

  • Use the properties of exponents, including rational exponents, and manipulate algebraic statements involving radicals.
  • Discriminate between equations and identities.

There is also an opportunity to consider the role of the imaginary number Syntax error from line 1 column 49 to line 1 column 73. Unexpected 'mathsize'., but this is optional.

Type: Lesson Plan

Original Student Tutorials

Solving Rational Equations: Cross Multiplying:

Learn how to solve rational linear and quadratic equations using cross multiplication in this interactive tutorial.

Type: Original Student Tutorial

The Radical Puzzle:

Learn to rewrite products involving radicals and rational exponents using properties of exponents in this interactive tutorial.

Type: Original Student Tutorial

Problem-Solving Tasks

Checking a Calculation of a Decimal Exponent:

In this example, students use properties of rational exponents and other algebraic concepts to compare and verify the relative size of two real numbers that involve decimal exponents.

Type: Problem-Solving Task

Rational or Irrational?:

This makes for a good follow-up task on rational irrational numbers after the students have been acquainted with some of the more basic properties, asking students to reason about rational and irrational numbers (N-RN.3) in a variety of ways. In addition to eliciting several different types of reasoning, the task requires students to rewrite radical expressions in which the radicand is divisible by a a perfect square.

Type: Problem-Solving Task

Tutorial

Power of a Power Property:

This tutorial demonstrates how to use the power of a power property with both numerals and variables.

Type: Tutorial

Unit/Lesson Sequence

Sample Algebra 1 Curriculum Plan Using CMAP:

This sample Algebra 1 CMAP is a fully customizable resource and curriculum-planning tool that provides a framework for the Algebra 1 Course. The units and standards are customizable and the CMAP allows instructors to add lessons, worksheets, and other resources as needed. This CMAP also includes rows that automatically filter and display Math Formative Assessments System tasks, E-Learning Original Student Tutorials and Perspectives Videos that are aligned to the standards, available on CPALMS.

Learn more about the sample Algebra 1 CMAP, its features and customizability by watching the following video:

Using this CMAP

To view an introduction on the CMAP tool, please .

To view the CMAP, click on the "Open Resource Page" button above; be sure you are logged in to your iCPALMS account.

To use this CMAP, click on the "Clone" button once the CMAP opens in the "Open Resource Page." Once the CMAP is cloned, you will be able to see it as a class inside your iCPALMS My Planner (CMAPs) app.

To access your My Planner App and the cloned CMAP, click on the iCPALMS tab in the top menu.

All CMAP tutorials can be found within the iCPALMS Planner App or at the following URL: http://www.cpalms.org/support/tutorials_and_informational_videos.aspx

Type: Unit/Lesson Sequence

Video/Audio/Animations

Rational Exponents:

Exponents are not only integers and unit fractions. An exponent can be any rational number expressed as the quotient of two integers.

Type: Video/Audio/Animation

Simplifying Radical Expressions:

Radical expressions can often be simplified by moving factors which are perfect roots out from under the radical sign.

Type: Video/Audio/Animation

MFAS Formative Assessments

Rational Exponents - 1:

Students are asked to convert numerical expressions from radical to exponential form.

Rational Exponents - 2:

Students are asked to convert numerical expressions from exponential to radical form.

Rational Exponents - 3:

Students are asked to convert a product of a radical and exponential expression to a single power of two.

Rational Exponents - 4:

Students are asked to rewrite expressions involving radicals and rational exponents in equivalent forms.

Original Student Tutorials Mathematics - Grades 9-12

Solving Rational Equations: Cross Multiplying:

Learn how to solve rational linear and quadratic equations using cross multiplication in this interactive tutorial.

The Radical Puzzle:

Learn to rewrite products involving radicals and rational exponents using properties of exponents in this interactive tutorial.

Student Resources

Vetted resources students can use to learn the concepts and skills in this benchmark.

Original Student Tutorials

Solving Rational Equations: Cross Multiplying:

Learn how to solve rational linear and quadratic equations using cross multiplication in this interactive tutorial.

Type: Original Student Tutorial

The Radical Puzzle:

Learn to rewrite products involving radicals and rational exponents using properties of exponents in this interactive tutorial.

Type: Original Student Tutorial

Problem-Solving Task

Checking a Calculation of a Decimal Exponent:

In this example, students use properties of rational exponents and other algebraic concepts to compare and verify the relative size of two real numbers that involve decimal exponents.

Type: Problem-Solving Task

Tutorial

Power of a Power Property:

This tutorial demonstrates how to use the power of a power property with both numerals and variables.

Type: Tutorial

Video/Audio/Animations

Rational Exponents:

Exponents are not only integers and unit fractions. An exponent can be any rational number expressed as the quotient of two integers.

Type: Video/Audio/Animation

Simplifying Radical Expressions:

Radical expressions can often be simplified by moving factors which are perfect roots out from under the radical sign.

Type: Video/Audio/Animation

Parent Resources

Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.

Problem-Solving Task

Checking a Calculation of a Decimal Exponent:

In this example, students use properties of rational exponents and other algebraic concepts to compare and verify the relative size of two real numbers that involve decimal exponents.

Type: Problem-Solving Task

Tutorial

Power of a Power Property:

This tutorial demonstrates how to use the power of a power property with both numerals and variables.

Type: Tutorial